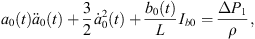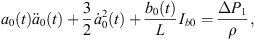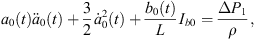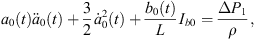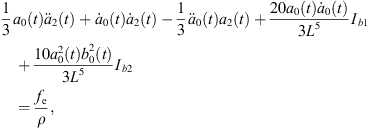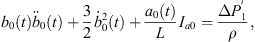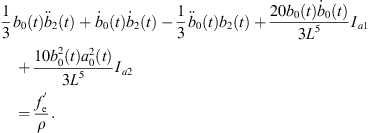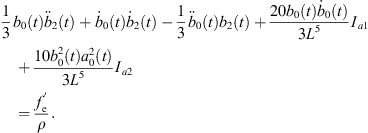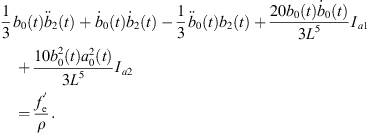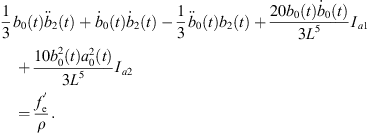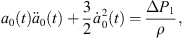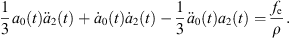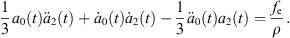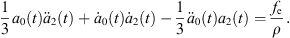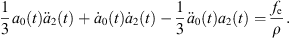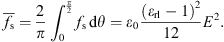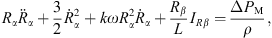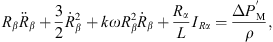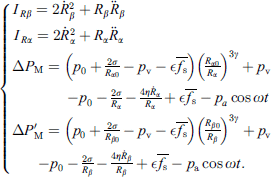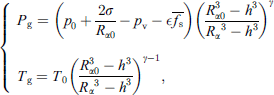| Issue |
Acta Acust.
Volume 6, 2022
|
|
|---|---|---|
| Article Number | 52 | |
| Number of page(s) | 9 | |
| Section | Ultrasonics | |
| DOI | https://doi.org/10.1051/aacus/2022048 | |
| Published online | 16 November 2022 | |
Scientific Article
Interaction between double nonspherical bubbles in compressible liquid under the coupling effect of ultrasound and electrostatic field
1
Department of Mechanical and Electrical Engineering, Yangjiang Polytechnic, Yangjiang 529500, China
2
School of Physics, South China University of Technology, Guangzhou 510640, China
3
Division of Quality Control, Yangtze Delta Region Institute of Tsinghua University, Jiaxing 314006, China
* Corresponding author: mingyufem@163.com
Received:
1
July
2022
Accepted:
27
October
2022
A dynamic model for a double-bubble system in compressible liquid under the coupling effect of ultrasound and electrostatic field was developed here. In this study, we mainly discussed the effect of the interaction on the investigated bubble using the numerical solutions to the theoretic model. The variable parameters are the distance between bubble centers and the initial radius of the adjacent bubble. In addition, we applied approximate equations to analyse variations of the internal gas pressure and temperature of a bubble. We found that, the oscillation amplitude of a bubble with an adjacent bubble significantly reduces, compared to that of an isolated bubble.
Key words: Ultrasound / Electrostatic field / Compressible liquid / Interaction double-bubble system
© The Author(s), published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Nomenclature
P2(cosθ): Second-order Legendre function
a0(t): Spherical radius component of bubble α
b0(t): Spherical radius component of bubble β
a2(t): Coefficient of nonspherical radius component of bubble α
b2(t): Coefficient of nonspherical radius component of bubble β
r α : Distance from a point in the liquid to the center of bubble α
r β : Distance from a point in the liquid to the center of bubble β
L : Distance between bubble centers
E : Electric field strength in the liquid region
p 0 : Static pressure of the liquid
p v : Vapor pressure in the bubble
p a : Acoustic pressure amplitude
σ : Surface tension at the liquid–gas interface
ω : Angular frequency of the acoustic wave
1 Introduction
As an efficient, environmentally-friendly and economical technology, the combination of an electric field with ultrasound has been widely used in laboratories and industrial fields in recent years. A study by Jung et al. [1] revealed that this combined treatment can be used to disintegrate waste activated sludge. After 60 min treatment time, the average particle size of the sludge decreased significantly more, compared to ultrasonic treatment alone. In addition, Yang et al. [2] used the ultrasound-synergized electric field extraction (UEE) to extract flavonoids from hemerocallis citrina baroni (a citron daylily). They found that the yield of flavonoids was 10% higher using UEE than conventional ultrasound extraction, and it was 18% higher than water bath extraction. A work by Yang et al. [3] reveals the mechanism how electric stress strengthens ultrasonic cavitation. However, many details of interactions between nonspherical bubbles are not known. In fact, when cavitation occurs in the liquid, it can generate a high number of cavitation bubbles, instead of a single one. The interactions between these adjacent bubbles affect the oscillation of the individual bubbles significantly, which should be considered in the mathematic model. To describe the effect of an adjacent bubble on the cavitation of an investigated bubble, we need to develop a dynamic equation-set including the interaction between double bubbles.
Many researchers helped advance the theoretical model for two interacting bubbles. Li et al. [4], Pityuk et al. [5], and Wang et al. [6] provided three different mathematical models for two adjacent spherical bubbles in an ultrasonic field. In the study of CCl4 sono-pyrolysis, Merouani et al. [7–9] used modified Keller-Miksis equations to analyze the thermal effect and the interaction between bubbles. Shima and Fujiwara [10] investigated the behavior of two spherical bubbles with different sizes near a solid wall and derived the motion equations for two bubbles. However, these models are unsuitable for two interacting nonspherical bubbles in the presence of an electric force. The variation of nonspherical radius components of bubbles cannot be obtained by simply modifying the models for spherical bubbles. Liang et al. [11] developed a dynamic model for two native nonspherical bubbles in an incompressible liquid. However, their derivation includes some important inaccuracies, which leads to incorrect mathematic equations. Furthermore, in the calculation of the total velocity potential near the interface of a bubble, they did not consider the perturbing velocity potential induced by the interaction between bubbles, which is an additional term of the total velocity potential. In addition, none of the above-mentioned studies considered the liquid’s compressibility. If the liquid’s compressibility is neglected in the numerical calculation, the maximum bubble-radius can easily be larger, and the minimum bubble-radius can be smaller, compared to the actual situation.
The present study aims to develop a dynamic model for nonspherical double-bubbles in a compressible liquid under the coupling effect of ultrasound and an electrostatic field. We used perturbation analysis, the sphere theorem, and the basic fluid-mechanics equations to derive the required model. We mainly analyze the effect of the interaction force on the investigated bubble using numerical solutions to the theoretical model. The variable parameters are: the distance between bubble centers, and the initial radius of the adjacent bubble. Furthermore, in the derivation, we offer an explanation why the effect of the liquid’s compressibility cannot transfer from the area near the interface of one bubble to the one of another bubble, when the two bubbles are far apart from each other. Finally, we applied approximate equations to investigate temporal evolutions of the gas pressure and the temperature inside a bubble. These results can provide better insights into the oscillation mechanism of interacting nonspherical bubbles in a compressible liquid.
2 Model for double nonspherical bubbles
2.1 Interface equations for double bubbles
To describe a double-bubble system, we introduce a nonspherical function S(θ, t) with rotational symmetry, which is independent of the rotation angle ϕ. In spherical coordinates, the interface equations for double bubbles can be expressed as
where
The small parameter ϵ indicates that, for both bubbles, the nonspherical components are much smaller than the spherical components.
Figure 1 shows the sections of two nonspherical bubbles, which are elliptic. The distance L is set to hundreds of microns in this study, namely L ≫ Sα + Sβ. The reason is that if two bubbles are too close, the coalescence of these two bubbles probably occurs. This is out of the scope of our discussion.
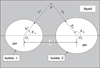 |
Figure 1 Sections of two nonspherical bubbles. |
2.2 Total pressure-difference on the whole liquid region outside a bubble
The direction of the electric field is set to parallel to the line of bubble centers. For an insulating bubble, the expression for electric stress fs [12, 13] is as follows:
The electric stress fs exerts on the bubble wall, stretching the bubble in the electric-field direction and compressing the bubble in the direction vertical to the electric field.
If a bubble undergoes adiabatic oscillation, the total pressure-difference on the whole liquid region outside this bubble can be written as
where
For a nonspherical bubble, R = a0(t) or b0(t). To simplify the calculation, the bubble is considered to be approximately spherical for the force analysis (Eqs. (6)–(8)). The rationality of this simplification is based on that the nonspherical term is much smaller than the spherical term for an elliptical bubble.
2.3 Derivation of the theoretical model
Let coordinates α be the spherical coordinates with the origin at the center of bubble α, and coordinates β be the spherical coordinates with the origin at the center of bubble β.
In coordinates α, the velocity potential of bubble α can be written as
where
Here, Φα0 (rα, t) and Φα2(rα, θα, t) are the spherical component and the nonspherical component of the velocity potential of bubble α. k is the wave number, k = ω/c, and c is the speed of sound in the liquid. A0(t) and A2(t) are two functions of time. The derivations of equations (10) and (11) (see Ref. [3]) are based on the assumption that ultrasonic wave propagates within an infinitely large liquid region. Hence, no standing wave occur in the liquid. This means that translational motions of bubbles cannot occur. Thus, the distance L can be considered constant.
In the dynamic model for bubble α, the interaction terms reflect the effects of bubble β on bubble α. The effect of the liquid’s compressibility only occurs in the vicinity of the interface of a bubble, which cannot transfer to the liquid region far away from the interface of a bubble. Importantly, this effect cannot transfer to the vicinity of the interface of another bubble, when the two bubbles are far apart from each other. The reason for this is as follows: In the radial direction, as the distance from a bubble center to a point in the liquid increases, the fluid velocity decreases sharply. The effect of the liquid’s compressibility is positively correlated with the fluid velocity. For a liquid region far away from the bubble interface, the fluid velocity is very small, the effect of the liquid’s compressibility can therefore be neglected. Hence, in the derivation of the dynamic model for bubble α, the liquid’s compressibility needs not to be considered when calculating the velocity potential of bubble β.
In coordinates β, the velocity potential of bubble β is
where
Here, Φβ0(rβ, t) and Φβ2(rβ, θβ, t) denote the spherical component and the nonspherical component of the velocity potential of bubble β. B0(t) and B2(t) are two functions of time. Equations (11) and (12) can be obtained from a study by Chen et al. [14].
To calculate the total velocity potential for a point in the liquid, we need to convert the expression of the velocity potential of bubble β from coordinates β to coordinates α. When rα is near the interface of bubble α, namely rα ≪ L, we have the following relations [15–19]:
where
and Pi(cosθα) is the ith-order Legendre function.
Substituting these relations into equations (11) and (12), we obtain the velocity potentials of bubble β in coordinates α:
In addition, according to the sphere theorem by Weiss [20], when bubble α exists in an arbitrary irrotational flow, it can cause a disturbance to this flow. Thus, an extra perturbing velocity potential can occur in the vicinity of the interface of bubble α. When the flow is undisturbed by bubble α, the unperturbed velocity potential of the flow should be Φβ. Hence, under the disturbance of bubble α, we denote the perturbing velocity potential as Φβ→α(rα, θα, t), which is also the additional velocity potential induced by bubble β in the vicinity of the interface of bubble α.
The perturbing velocity potential can be calculated by the following equality [20]:
Substituting equations (15) and (16) into the above equality, we obtain
Similarly, Φα→β(rα, θα, t) represents the perturbing velocity potential induced by bubble α in the vicinity of the interface of bubble β. However, we assume that L ≫ Sα + Sβ. Thus, the effect of Φα→β(rα, θα, t) on the vicinity of the interface of bubble α is extremely small. By calculation, we can formulate Φα→β(rα, θα, t) = O(1/L10) in coordinates α. Hence, the term Φα→β(rα, θα, t) can be neglected for the calculation of the total velocity potential.
In addition, the total velocity potential Φ(rα, θα, t) should be consistent with the radius function of bubble α (see Eqs. (1a)) in form. Thus, in the nonspherical term of Φ(rα, θα, t), only the terms about the second-order Legendre function P2(cosθα) can be retained. The expression for the total velocity potential is:
At the interface of bubble α, the total velocity potential satisfies the following two equations:
where the expression of ΔP see equation (4). Equation (20) is obtained when the gravity of the liquid is negligible and the liquid flow is irrotational. Substituting equations (1a) and (18) into equations (19) and (20), using the Taylor series expansion of ϵ, and only retaining the first two order terms for ϵ, we obtain
At the interface of bubble β, the total velocity potential satisfies the following equation [20]:
Substituting equations (1b) and (10)–(12) into equation (25), using the Taylor series expansion of ϵ, and neglecting the Peano remainder 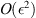 , we obtain
, we obtain
Here, the liquid’s compressibility is not considered.
Let Rα0 and Rβ0 be initial radii of bubble α and bubble β, namely Rα0 = a0(0) and Rβ0 = b0(0). After eliminating A0(t), A2(t), B0(t), B2(t), and their derivatives from the equations consisted by equations (21)–(24) and equations (26)–(27), we obtain the model for bubble α under the action of bubble β:
where
Equation (28a) is a modified Rayleigh-Plesset equation for a0(t). The term 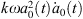 is related to the oscillation resistance induced by the liquid’s compressibility. Equation (28b) can be regarded as a damped vibration equation for a2(t) with external forces, without consideration of time-varying coefficients. In addition, all terms for L are related to the forces that bubble β exerts on bubble α.
is related to the oscillation resistance induced by the liquid’s compressibility. Equation (28b) can be regarded as a damped vibration equation for a2(t) with external forces, without consideration of time-varying coefficients. In addition, all terms for L are related to the forces that bubble β exerts on bubble α.
Following similar steps, we can also obtain the model for bubble β under the action of bubble α, which has a similar form as the model for bubble α.
where
When c →∞, namely k → 0, equations (28a)–(28b) and equations (29a)–(29b) are reduced to the equations for an incompressible liquid,
When L → ∞, equations (30a) and (30b) can be further reduced to the equations for a single nonspherical bubble, see equations (32a) and (32b).
3 Numerical solutions and analysis
3.1 Effect of the distance between bubble centers on the radius of bubble α
By solving equations (28a)–(28b) and equations (29a)–(29b) numerically, we obtain the temporal evolutions of the spherical coefficient a0(t) and the nonspherical coefficient a2(t) of bubble α at different distances between bubble centers (see Figs. 2 and 3). In these two figures, the condition L → ∞ represents the oscillation of an isolated nonspherical bubble. The other parameters see Table 1.
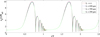 |
Figure 2 Temporal evolution of a0(t) at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm). |
 |
Figure 3 (a) Temporal evolution of a2(t) at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm); (b) Partial enlarged detail of (a). |
Simulation parameters.
In Figure 2, the variations of a0(t) with time, at different distances L, have a similar pattern. Within one period, a0(t) first increases rapidly to its maximum during the rarefaction cycle, then, it decreases sharply to its minimum in a rather short time. This is followed by a series of rebounds. Furthermore, as the distance between two bubbles increases, the maximum of a0(t) increases, and, correspondingly, the minimum of a0(t) decreases. When L → ∞, a0(t) reaches its highest maximum and lowest minimum. In Figure 3, a2(t) shows exponential increases with time during the first period. Theoretically, a2(t) shows a larger increase at a longer distance L. In other words, when the distance between bubble centers is longer, bubble α is subject to lower oscillation resistance from bubble β, and appears to be more ellipsoidal. The similar time-varying curves of a2(t) were also reported by Liang et al. [11, 21, 22] and Chen et al. [14].
3.2 Effect of the initial radius of bubble β on the radius of bubble α
When the distance is fixed at L = 350 μm, and the value of Rβ0 is variable, we can solve the equations (28a)–(28b) and equations (29a)–(29b) numerically and obtain time-varying curves of two radius components of bubble α. All parameters are the same as in Section 3.1. As depicted in Figure 4, when Rβ0 ≤ 3.5 μm, the wave peaks of a0(t) increase, while Rβ0 is increasing. However, as the initial radius Rβ0 increases from 3.5 μm to 6 μm, the wave peaks of a0(t) decrease significantly. Hence, the highest maximum and the lowest minimum of a0(t) occur when Rβ0 = 3.5 μm. Moreover, the spherical component a0(t) undergoes faster oscillation damping for smaller Rβ0 values. Figure 5 reveals that, when bubble β has a higher initial radius Rβ0, the coefficient a2(t) shows a lower increase during one oscillation period. This means that the nonspherical feature of bubble α is more significant for smaller Rβ0 values.
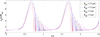 |
Figure 4 Temporal evolution of a0(t) for different initial radii of bubble β (T = 50 μs, Rα0 = 4.5 μm). |
 |
Figure 5 Temporal evolution of a2(t) for different initial radii of bubble β (T = 50 μs, Rα0 = 4.5 μm). |
3.3 Analyses of the cavitation of bubble α using approximate equations
These rapid increases of the coefficient a2(t), as shown in Figures 3 and 5, are unlikely to occur physically. In fact, it is impossible for a2(t) to increase without limits. This can be interpreted as follows: A nonspherical bubble has already collapsed before its nonspherical coefficient a2(t) reaches such a large value. The variation curves of a2(t) are only the results of the numerical solution to dynamic equations. Thus, to further investigate the effect of bubble β during the cavitation of bubble α, we introduce approximate equations. The method is to take the mean of electric stress fs in half period, and approximately transform a nonspherical bubble into a spherical bubble. The reason for adopting this method is as follows: the presence of electric stress reduces the surface tension at a bubble wall, which causes a bubble to expand more during the rarefaction cycle. Therefore, it is more suitable to take the mean of electric stress fs in half period, rather than the mean of the bubble radius S(θ, t) in half period. A nonspherical bubble should be approximately treated as a spherical bubble with smaller surface tension, instead of a spherical bubble with a larger initial radius.
The mean of fs in half period is
Let Rα and Rβ be radii of approximate spherical bubbles of bubble α and bubble β. By inserting the term 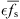 into the right sides of equations (28a) and (29a) and replacing a0(t) and b0(t) with Rα and Rβ, we can rewrite equations (28a) and (29a) as
into the right sides of equations (28a) and (29a) and replacing a0(t) and b0(t) with Rα and Rβ, we can rewrite equations (28a) and (29a) as
where
The equations (34a) and (34b) are the approximate equations that describe the radius variations of bubble α and bubble β with the interaction between two bubbles. To simplify the calculation, we assume that ϵ = 0.1 in the following analysis. As long as ϵ > 0, all conclusions below do not change with the ϵ value.
3.3.1 Effect of bubble β on the radius of bubble α
In Section 3.2, we concluded that, when Rβ0 = 3.5 μm, a0(t) reaches its highest maximum and lowest minimum. Thus, the numerical solutions of equations (34a) and (34b) are performed for the bubble pair with initial radii Rα0 = 4.5 μm and Rβ0 = 3.5 μm. All other parameters are the same as in Section 3.1. Figure 6 shows the temporal evolution of Rα at different distances between two bubbles. The condition L → ∞ reflects the oscillation of an isolated bubble. With increasing distance between bubble centers, the oscillation amplitude of the radius of bubble α increases. This can be explained as follows: A longer distance between bubble centers leads to less oscillation resistance and higher expansion during the rarefaction cycle for bubble α. During the compression cycle, bubble α with a larger maximum radius undergoes a more violent collapse, and it therefore reaches a lower minimum radius. Hence, the highest maximum radius and the lowest minimum radius are obtained during the oscillation of an isolated bubble.
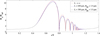 |
Figure 6 Temporal evolution of Rα at different distances between bubble centers (L) (T = 50 μs, Rα0 =4.5 μm). |
3.3.2 Effect of bubble β on the gas pressure and the temperature inside bubble α
When the van der Waals hard-core radius h is taken into account, the expressions for the gas pressure Pg and the temperature Tg in the center of bubble α are given by [23, 24]
where T0 is the ambient temperature, T0 = 298.15 K. For bubble α with an initial radius Rα0 = 4.5 μm, h = Rα0/8.54 ≈ 0.53 μm. As shown in Figures 7 and 8, under all conditions, the maximum gas-pressure and temperature inside bubble α occur at the end of the collapse, when bubble α reaches its minimum radius. Furthermore, during the negative pressure phase of the ultrasound wave, the maximum internal pressure and temperature of an isolated bubble are significantly higher, compared to a bubble with another adjacent bubble. In general, regardless of the distance between two bubbles and the initial radius of an adjacent bubble, the interaction between two bubbles always acts as resistance to the oscillation of a bubble, when parameters of ultrasound and an electrostatic field are constant.
 |
Figure 7 Temporal evolution of Pg at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm, p0 = 1.013 × 105 Pa). |
 |
Figure 8 Temporal evolution of Tg at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm, T0 = 298.15 K). |
4 Conclusion
In the present study, we developed a model for two interacting nonspherical bubbles in a compressible liquid under the coupling effect of ultrasound and electrostatic field. When the distance between bubble centers is shorter, bubble α is subject to higher oscillation resistance from bubble β, and appears to be more ellipsoidal. When the initial radius Rβ0 equals to 3.5 μm, a0(t) reaches its highest maximum and lowest minimum. For a larger Rβ0 value, the nonspherical feature of bubble α becomes more significant after several periods. By solving approximate equations numerically, we found that, at the end of the collapse, the maximum pressure and temperature inside an isolated bubble are significantly higher than a bubble with an adjacent bubble. However, this obtained model can only depict the interaction between two adjacent bubbles. In fact, when a number of bubbles undergo ultrasonic cavitation simultaneously, the interaction between them can be more complicated. Therefore, a subject of our future research could be the oscillation of a nonspherical bubble cluster, as well as the effect of the interaction on the resonance frequency of the investigated bubble.
Acknowledgments
This research were supported by Provincial Major Project in Basic and Applied Research of Natural Science (Department of Education of Guangdong Province) (No.2017GKZDXM015), National Natural Science Foundation of China (No.11464002), Innovation Team Project of Colleges and Universities in Guangdong Province (Natural Science) (No.2020KCXTD054), Key Scientific Research Platform of Colleges and Universities (Department of Education of Guangdong Province) (No.2021GCZX017), Special Project in Key Fields of Universities in Guangdong Province (Science and Technology Services for Rural Revitalization) (No.2022ZDZX4118), and Youth Innovation Talent Project of Universities in Guangdong Province (No.2022KQNCX261).
Data Availability Statement
The research data associated with this article are included within the article.
References
- K.-W. Jung, M.-J. Hwang, M.-J. Cha, K.-H. Ahn: Application and optimization of electric field-assisted ultrasonication for disintegration of waste activated sludge using response surface methodology with a Box-Behnken design. Ultrasonics Sonochemistry 22 (2015) 437–445. [CrossRef] [PubMed] [Google Scholar]
- R.-F. Yang, L.-L. Geng, H.-Q. Lu, X.-D. Fan: Ultrasound-synergized electrostatic field extraction of total flavonoids from hemerocallis citrina baroni. Ultrasonics Sonochemistry 34 (2017) 571–579. [CrossRef] [PubMed] [Google Scholar]
- J.-J. Deng, R.-F. Yang, H.-Q. Lu: Dynamics of nonspherical bubble in compressible liquid under the coupling effect of ultrasound and electrostatic field. Ultrasonics Sonochemistry 71 (2021). [Google Scholar]
- F. Li, J. Cai, X. Huai, B. Liu: Interaction mechanism of double bubbles in hydrodynamic cavitation. Journal of Thermal Science 22, 3 (2013) 242–249. [CrossRef] [Google Scholar]
- Y. Pityuk, N. Gumerov, O. Abramova, I. Zarafutdinov, I. Akhatov: Numerical study of interaction of two deformable bubbles in an acoustic field. Journal of Applied Mechanics and Technical Physics 60, 4 (2019) 661–668. [CrossRef] [Google Scholar]
- C. Wang, J. Cheng: The velocity field around two interacting cavitation bubbles in an ultrasound field. Science China-Physics Mechanics & Astronomy 56 (2013) 1246–1252. [CrossRef] [Google Scholar]
- A. Dehane, S. Merouani: Impact of dissolved rare gases (ar, xe and he) on single-bubble sonochemistry in the presence of carbon tetrachloride. Chemical Papers 76, 5 (2022) 3011–3030. [CrossRef] [Google Scholar]
- A. Dehane, S. Merouani, O. Hamdaoui, M.H. Abdellattif, B.-H. Jeon, Y. Benguerba: A full mechanistic and kinetics analysis of carbon tetrachloride (ccl4) sono-conversion: Liquid temperature effect. Journal of Environmental Chemical Engineering 9, 6 (2021). [Google Scholar]
- A. Dehane, S. Merouani, O. Hamdaoui, M. Ashokkumar: An alternative technique for determining the number density of acoustic cavitation bubbles in sonochemical reactors. Ultrasonics Sonochemistry 82 (2022) 105872. [CrossRef] [PubMed] [Google Scholar]
- A. Shima, T. Fujiwara: The behavior of two bubbles near a solid wall. Archive of Applied Mechanics 62, 1 (1992) 53–61. [CrossRef] [Google Scholar]
- J.-F. Liang, W.-Z. Chen, W.-H. Shao, S.-B. Qi: Aspherical oscillation of two interacting bubbles in an ultrasound field. Chinese Physics Letters 29, 7 (2012) 074701. [CrossRef] [Google Scholar]
- M.C. Zaghdoudi, M. Lallemand: Study of the behaviour of a bubble in an electric field: steady shape and local fluid motion. International Journal of Thermal Sciences 39, 1 (2000) 39–52. [CrossRef] [Google Scholar]
- J.R. Reitz, F.J. Milford, R.W. Christy: Foundations of Electromagnetic Theory (4th edn.). Addison-Wesley Publishing Company, 2008. [Google Scholar]
- W.-J. Wang, W.-Z. Chen, M.-J. Lu, R.-J. Wei: Bubble oscillations driven by aspherical ultrasound in liquid. Journal of the Acoustical Society of America 114, 4 (2003) 1898–1904. [CrossRef] [PubMed] [Google Scholar]
- A.A. Doinikov: Translational motion of two interacting bubbles in a strong acoustic field. Physical Review E 64, 2 (2001) 026301. [CrossRef] [Google Scholar]
- A.A. Doinikov, A. Bouakaz: Theoretical model for coupled radial and translational motion of two bubbles at arbitrary separation distances. Physical Review E 92, 4 (2015) 043001. [CrossRef] [PubMed] [Google Scholar]
- D.A. Varshalovich, A.N. Moskalev, V.K. Khersonsky: The quantum theory of angular momentum. World Scientific Publishing Co., Pte. Ltd., 1988. [CrossRef] [Google Scholar]
- M.L. Boas: Mathematical methods in the physical sciences (2nd edn.). John Wiley & Sons Inc., 1983. [Google Scholar]
- K.F. Riley, M.P. Hobson, S.J. Bence: Mathematical methods for physics and engineering: a comprehensive guide (3rd edn.). Cambridge University Press, 2006. [CrossRef] [Google Scholar]
- P. Weiss: On hydrodynamical images. arbitrary irrotational flow disturbed by a sphere. Mathematical Proceedings of the Cambridge Philosophical Society 40, 3 (1944) 259–261. [CrossRef] [Google Scholar]
- J.-F. Liang, X. Wang, J. Yang, L. Gong: Dynamics of two interacting bubbles in a nonspherical ultrasound field. Ultrasonics 75 (2017) 58–62. [CrossRef] [PubMed] [Google Scholar]
- J.-F. Liang, X. Wu, Y. Qiao: Dynamics of twin bubbles formed by ultrasonic cavitation in a liquid. Ultrasonics Sonochemistry 80 (2021) 105837. [CrossRef] [PubMed] [Google Scholar]
- T. Hongray, B. Ashok, J. Balakrishnan: Oscillatory dynamics of a charged microbubble under ultrasound. Pramana 84, 4 (2015) 517–541. [CrossRef] [Google Scholar]
- M.P. Brenner, S. Hilgenfeldt, D. Lohse: Single-bubble sonoluminescence. Reviews of Modern Physics 74 (2002) 425–484. [CrossRef] [Google Scholar]
Cite this article as: Deng J-J. Yu M. & Yang R-F. 2022. Interaction between double nonspherical bubbles in compressible liquid under the coupling effect of ultrasound and electrostatic field. Acta Acustica, 6, 52.
All Tables
All Figures
 |
Figure 1 Sections of two nonspherical bubbles. |
| In the text | |
 |
Figure 2 Temporal evolution of a0(t) at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm). |
| In the text | |
 |
Figure 3 (a) Temporal evolution of a2(t) at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm); (b) Partial enlarged detail of (a). |
| In the text | |
 |
Figure 4 Temporal evolution of a0(t) for different initial radii of bubble β (T = 50 μs, Rα0 = 4.5 μm). |
| In the text | |
 |
Figure 5 Temporal evolution of a2(t) for different initial radii of bubble β (T = 50 μs, Rα0 = 4.5 μm). |
| In the text | |
 |
Figure 6 Temporal evolution of Rα at different distances between bubble centers (L) (T = 50 μs, Rα0 =4.5 μm). |
| In the text | |
 |
Figure 7 Temporal evolution of Pg at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm, p0 = 1.013 × 105 Pa). |
| In the text | |
 |
Figure 8 Temporal evolution of Tg at different distances between bubble centers (L) (T = 50 μs, Rα0 = 4.5 μm, T0 = 298.15 K). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



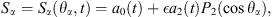
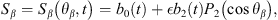
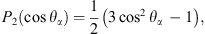
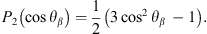
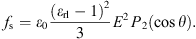
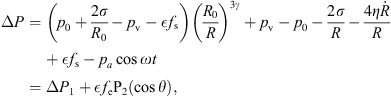
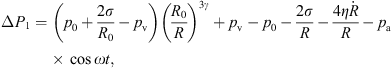
![$$ {f}_{\mathrm{e}}=\left[1-{\left(\frac{{R}_0}{R}\right)}^{3\gamma }\right]{\epsilon }_0\frac{{\left({\epsilon }_{\mathrm{r}\mathrm{l}}-1\right)}^2}{3}{E}^2. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq9.gif)
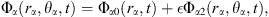
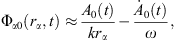
![$$ {\mathrm{\Phi }}_{\alpha 2}\left({r}_{\alpha },{\theta }_{\alpha },t\right)\approx {P}_2\left(\mathrm{cos}{\theta }_{\alpha }\right)\left[\frac{3{A}_2(t)}{{k}^3{r}_{\alpha }^3}+\frac{2{A}_2(t)}{k{r}_{\alpha }}+\frac{{\dot{A}}_2(t)}{\omega }\right]. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq12.gif)
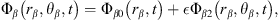
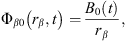
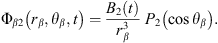
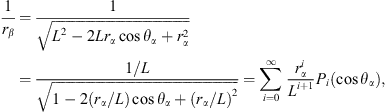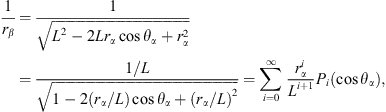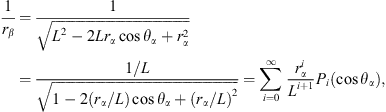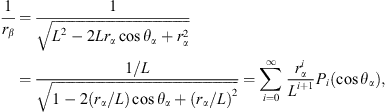
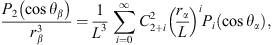
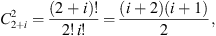
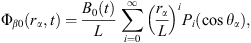
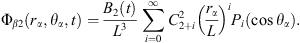
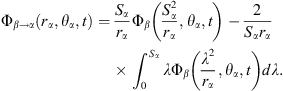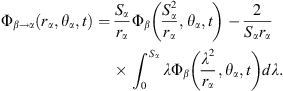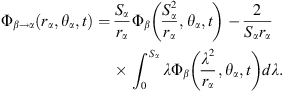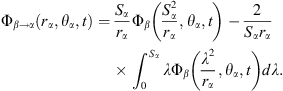
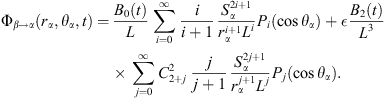
![$$ \mathrm{\Phi }({r}_{\alpha },{\theta }_{\alpha },t)={\mathrm{\Phi }}_{\alpha }({r}_{\alpha },{\theta }_{\alpha },t)+{\mathrm{\Phi }}_{\beta }({r}_{\alpha },{\theta }_{\alpha },t)+{\mathrm{\Phi }}_{\beta \to \alpha }({r}_{\alpha },{\theta }_{\alpha },t)\approx \frac{{A}_0(t)}{k{r}_{\alpha }}-\frac{{\dot{A}}_0(t)}{\omega }+\frac{{B}_0(t)}{L}+\epsilon {P}_2(\mathrm{cos}{\theta }_{\alpha })\left\{\frac{3{A}_2(t)}{{k}^3{r}_{\alpha }^3}+\frac{2{A}_2(t)}{k{r}_{\alpha }}+\frac{{\dot{A}}_2(t)}{\omega }\left.+\frac{{B}_2(t)}{{L}^5}\left[6{r}_{\alpha }^2+\frac{4{S}_{\alpha }^5}{{r}_{\alpha }^3}\right]\right\}.\right. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq23.gif)
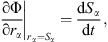
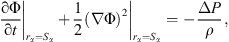
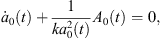
![$$ {\dot{a}}_2(t)-\frac{2{a}_2(t)}{k{a}_0^3(t)}{A}_0(t)+\left[\frac{9}{{k}^3{a}_0^4(t)}+\frac{2}{k{a}_0^2(t)}\right]{A}_2(t)=0, $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq30.gif)
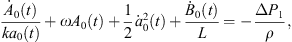
![$$ \frac{\left[3+2{k}^2{a}_0^2(t)\right]{\dot{A}}_2(t)}{{k}^3{a}_0^3(t)}-\omega {A}_2(t)-\frac{{a}_2(t){\dot{A}}_0(t)}{k{a}_0^2(t)}+{\dot{a}}_0(t){\dot{a}}_2(t)+\frac{20{a}_0(t){\dot{a}}_0(t)}{{L}^5}{B}_2(t)+\frac{10{a}_0^2(t)}{{L}^5}{\dot{B}}_2(t)=-\frac{{f}_{\mathrm{e}}}{\rho }. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq32.gif)
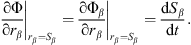
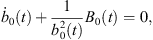
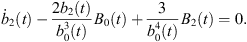
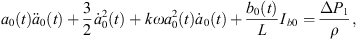
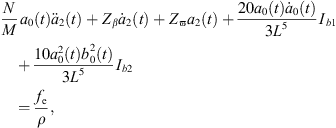
![$$ \left\{\begin{array}{ll}& \enspace k=\frac{\omega }{c}\\ & \enspace M=9+2{k}^2{a}_0^2(t)\\ & \enspace N=3+2{k}^2{a}_0^2(t)\\ & \enspace {Z}_{\beta }=\left[\frac{6N-M}{M}-\frac{4{k}^2{a}_0^2(t)N}{{M}^2}\right]{\dot{a}}_0(t)-\frac{{k}^3\omega {a}_0^4(t)}{M}\\ & \enspace {Z}_{\varpi }=\left(\frac{6N}{M}-2\right)\frac{{\dot{a}}_0^2(t)}{{a}_0(t)}+\left(\frac{2N}{M}-1\right){\ddot{a}}_0(t)\\ & \enspace -\frac{8{k}^2{a}_0(t){\dot{a}}_0^2(t)N}{{M}^2}-\frac{2{k}^3\omega {a}_0^3(t){\dot{a}}_0(t)}{M}\\ & \enspace {I}_{b0}=2{\dot{b}}_0^2(t)+{b}_0(t){\ddot{b}}_0(t)\\ & \enspace {I}_{b1}={b}_0^3(t)\left[2{\dot{b}}_0(t){b}_2(t)+{b}_0(t){\dot{b}}_2(t)\right]\\ & \enspace {I}_{b2}=6{\dot{b}}_0^2(t){b}_2(t)+2{b}_0(t){\ddot{b}}_0(t){b}_2(t)\\ & \enspace +6{b}_0(t){\dot{b}}_0(t){\dot{b}}_2(t)+{b}_0^2(t){\ddot{b}}_2(t)\\ & \enspace \Delta {P}_1=\left({p}_0+\frac{2\sigma }{{R}_{\alpha 0}}-{p}_{\mathrm{v}}\right){\left[\frac{{R}_{\alpha 0}}{{a}_0(t)}\right]}^{3\gamma }+{p}_{\mathrm{v}}-{p}_0\\ & \enspace -\frac{2\sigma }{{a}_0(t)}-\frac{4\eta {\dot{a}}_0(t)}{{a}_0(t)}-{p}_{\mathrm{a}}\mathrm{cos}{\omega t}\\ & \enspace {f}_{\mathrm{e}}=\left\{1-{\left[\frac{{R}_{\alpha 0}}{{a}_0(t)}\right]}^{3\gamma }\right\}{\epsilon }_0\frac{{\left({\epsilon }_{\mathrm{r}\mathrm{l}}-1\right)}^2}{3}{E}^2.\end{array}\right. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq40.gif)
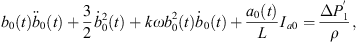
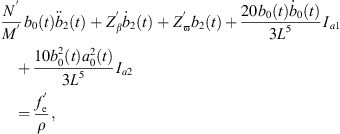
![$$ \left\{\begin{array}{ll}& \enspace {M}^\mathrm{\prime}=9+2{k}^2{b}_0^2(t)\\ & \enspace {N}^\mathrm{\prime}=3+2{k}^2{b}_0^2(t)\\ & \enspace {Z}_{\beta }^\mathrm{\prime}=\left[\frac{6{N}^\mathrm{\prime}-{M}^\mathrm{\prime}}{{M}^\mathrm{\prime}}-\frac{4{k}^2{b}_0^2(t){N}^\mathrm{\prime}}{{\left({M}^\mathrm{\prime}\right)}^2}\right]{\dot{b}}_0(t)-\frac{{k}^3\omega {b}_0^4(t)}{{M}^\mathrm{\prime}}\\ & \enspace {Z}_{\varpi }^\mathrm{\prime}=\left(\frac{6{N}^\mathrm{\prime}}{{M}^\mathrm{\prime}}-2\right)\frac{{\dot{b}}_0^2(t)}{{b}_0(t)}+\left(\frac{2{N}^\mathrm{\prime}}{{M}^\mathrm{\prime}}-1\right){\ddot{b}}_0(t)\\ & \enspace -\frac{8{k}^2{b}_0(t){\dot{b}}_0^2(t){N}^\mathrm{\prime}}{{\left({M}^\mathrm{\prime}\right)}^2}-\frac{2{k}^3\omega {b}_0^3(t){\dot{b}}_0(t)}{{M}^\mathrm{\prime}}\\ & \enspace {I}_{a0}=2{\dot{a}}_0^2(t)+{a}_0(t){\ddot{a}}_0(t)\\ & \enspace {I}_{a1}={a}_0^3(t)\left[2{\dot{a}}_0(t){a}_2(t)+{a}_0(t){\dot{a}}_2(t)\right]\\ & \enspace {I}_{a2}=6{\dot{a}}_0^2(t){a}_2(t)+2{a}_0(t){\ddot{a}}_0(t){a}_2(t)\\ & \enspace +6{a}_0(t){\dot{a}}_0(t){\dot{a}}_2(t)+{a}_0^2(t){\ddot{a}}_2(t)\\ & \enspace \Delta {P}_1^\mathrm{\prime}=\left({p}_0+\frac{2\sigma }{{R}_{\beta 0}}-{p}_{\mathrm{v}}\right){\left[\frac{{R}_{\beta 0}}{{b}_0(t)}\right]}^{3\gamma }+{p}_{\mathrm{v}}-{p}_0\\ & \enspace -\frac{2\sigma }{{b}_0(t)}-\frac{4\eta {\dot{b}}_0(t)}{{b}_0(t)}-{p}_{\mathrm{a}}\mathrm{cos}{\omega t}\\ & \enspace {f}_{\mathrm{e}}^\mathrm{\prime}=\left\{1-{\left[\frac{{R}_{\beta 0}}{{b}_0(t)}\right]}^{3\gamma }\right\}{\epsilon }_0\frac{{\left({\epsilon }_{\mathrm{r}l}-1\right)}^2}{3}{E}^2.\end{array}\right. $$](/articles/aacus/full_html/2022/01/aacus220054/aacus220054-eq44.gif)