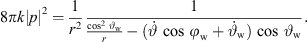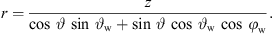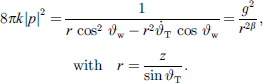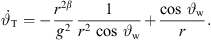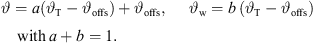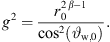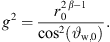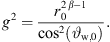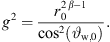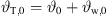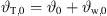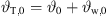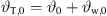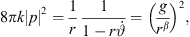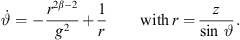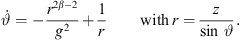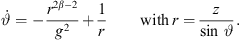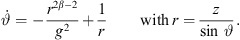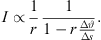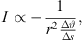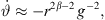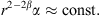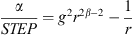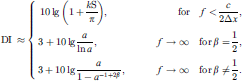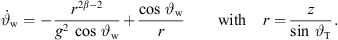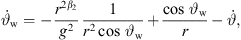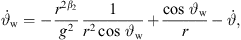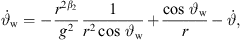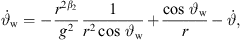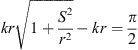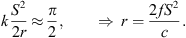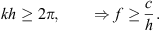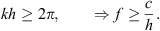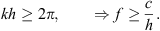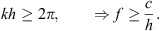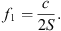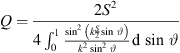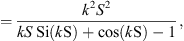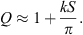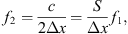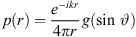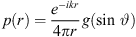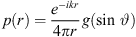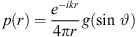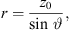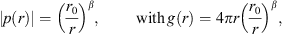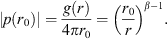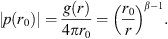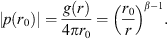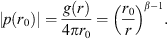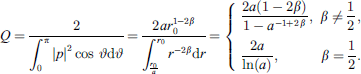| Issue |
Acta Acust.
Volume 7, 2023
|
|
|---|---|---|
| Article Number | 52 | |
| Number of page(s) | 12 | |
| Section | Audio Signal Processing and Transducers | |
| DOI | https://doi.org/10.1051/aacus/2023045 | |
| Published online | 27 October 2023 | |
Scientific Article
Theory of continuously curved and phased line sources for sound reinforcement
Institute of Electronic Music and Acoustics, University of Music and Performing Arts Graz, 8010 Graz, Austria
* Corresponding author: goelles@iem.at
Received:
24
April
2023
Accepted:
6
September
2023
To supply large audience areas uniformly with amplified direct sound, large-scale sound reinforcement often employs line-source loudspeaker arrays adapted to the listening area by either adjusting the angles or delays between their individual elements. This paper proposes a model for such or smaller line-source loudspeakers based on a delayed Green’s function integrated over an unknown contour. For a broad frequency range, stationary phase approximation yields a differential equation that we utilize to find a curve and delay progression providing direct sound levels rolling off with −6β dB per doubling of the distance; curve and phase designs can also be mixed to meet simultaneous targets using multiple design parameters β. The effectiveness of the formalism is proven by simulations of coverage, directivity, and discretization artifacts. Measurements on a miniature line array prototype that targets medium-scale immersive sound reinforcement applications verify the proposed theory for curvature, delay, and mixed designs.
Key words: Line source loudspeaker arrays / Sound reinforcement / Stationary phase approximation / Delay beamforming / Curvilinear arrays
© The Author(s), Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
One of the big challenges for sound reinforcement is to provide high-quality sound for the largest parts of a predefined audience area [1]. High-quality, high-power supply of large audience areas with consistently reinforced sound pressure levels has been considering line-source loudspeaker arrays driven by identical signals for several decades, nowadays. The wavefront sculpture technology (WST [2, 3]) as contemporary line-source theory is based on adjusting the length of the most relevant, binary Fresnel zone for all distances from the stage. Despite the simplicity of its model and a handful of criteria it needs, it provides a powerful and practical theory for line-source loudspeaker arrays. Furthermore, Straube et al. [4, 5], Hölter et al. [6] and Thompson et al. [7–9] discuss the modeling and optimization of the line-source array curvature to obtain tilt angles between the discrete elements, adapted to the listening area. Line-source arrays could also be applied in surround sound applications, and for instance Toole [10] of p. 330 describes the application of line sources compared to point-source loudspeaker setups.
As an alternative way to obtain a desired sound level curve over the listening area, beamforming based on constrained least square optimization was suggested by Beuningen et al. [11]. Beamformers can be found in applications with microphone arrays [12] and with loudspeaker arrays [13–15], and they require individual delays and amplification per transducer, often also filtering.
Moreover, delay and sum beamformers, or phased arrays as they are called when used for narrow-band signals, are also found in antenna theory, radar applications, or optics [16–18]. For a linear antenna array, Shanks [19] applied the stationary phase approximation to determine from the array’s radiation integral the phase and amplitude function required to form a cosecant-squared beam. Chiang et al. [20] used the same approximation method to estimate the beampatterns of in-phase curvilinear arrays, and Chakraborty et al. [21] applied the approximation to a linear array, obtained and solved a first-order differential equation, e.g., to form a cosecant beam. The cosecant beam is equivalent to a 0 dB attenuation target per doubling of the distance, when employing a vertical array below/above a horizontal plane.
Stationary-phase approximation has not only proven to be a powerful tool in antenna beamforming, but it is also used in wave field synthesis [22–24] and yields relatively simple signal processing (gains, delays, common pre-filter). What is more, Schultz [25] suggested the Fourier transform and wave field synthesis as theoretical background for line-source loudspeaker arrays.
In cinema sound practice, SMPTE RP 2096-1 [26] defines a rectangular area of roughly a third of the radius (±1/5 times the width by ±1/6 times the depth of a hall), in which the loudspeaker sound level should be flat within ±3 dB. This confines the maximum mixing imbalance of directional sounds to 6 dB in this area and is still soft enough to accept the mixing imbalance at off-center listening positions accomplished by two ideal point source loudspeakers in the free field, at opposite sides. Providing for a more constant coverage with distance, Nettingsmeier et al. [27] demonstrated an enlarged listening area (sweet area), when using eight short line-source arrays for third-order ambisonic surround play-back. Gölles et al. [28] showed that curved line sources designed for a direct-sound coverage of 0 dB attenuation per doubling of the distance potentially improves directional localization in a large listening area, above a length-dependent frequency limit. For less perfect coverage targets, Zotter et al. [29] found that direct sound objects rendered with −1 dB roll-off per doubling of the distance may limit the mixing imbalances acceptably (≤3 dB) within 75% of the loudspeaker layout’s radius. For a large listening area preserving the envelopment of a diffuse sound scene, by contrast, a substantially different optimal coverage criterion was found by Riedel et al. [30, 31], requiring that horizontally surrounding loudspeakers should exhibit a −3 dB attenuation per doubling of the distance for optimal results.
We propose an extended theoretical basis for the design of line-source curving and phasing. Its result is broadband for line sources that are (i) sufficiently tall, cf. equation (A.1), and (ii) densely spaced, cf. equation (A.2), or waveguided. The target is to support desired sound-pressure roll-off profiles of −6β dB per doubling of distance based on either curvature or delay, or both, and potentially multiple of such profiles, simultaneously, with the design parameter β. The proposed theory employs a stationary-phase-approximated contour integral over delayed Green’s functions and yields a second-order nonlinear differential equation. We propose two algorithms to numerically find optimal geometry and delay curves, followed by simulation studies and measurements on a miniature line array prototype as a proof of concept.
2 Continuous curvature and phase
We evaluate the sound pressure p of a curved source fed by a progressive time delay τ given as length w = c τ by an integral of a Green’s function 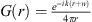 over the natural length parameter s of the unknown source contour C,
over the natural length parameter s of the unknown source contour C,
The imaginary unit i yields i2 = −1, the wave number is 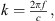 the speed of sound is c = 343 m/s, and f is the regarded frequency.
the speed of sound is c = 343 m/s, and f is the regarded frequency.
2.1 Integrals defining contour and delay
We define the convex curve ![$ {x}\left(\mathrm{s}\right)={\left[\begin{array}{ccc}x(s)& 0& z(s)\end{array}\right]}^T$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq9.gif) as parametric curve depending on the inclination angle
as parametric curve depending on the inclination angle 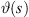 at every length coordinate s on the source, cf. Figure 1,
at every length coordinate s on the source, cf. Figure 1,
and the distance to a receiver at ![$ {{x}}_{\mathrm{r}}={\left[\begin{array}{ccc}{x}_{\mathrm{r}}& {y}_{\mathrm{r}}& 0\end{array}\right]}^T$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq14.gif) is
is
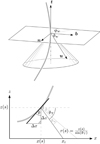 |
Figure 1 Continuous arc-shaped source (solid grey) with accompanying Frenet trihedron (top) at the point |
Moreover, w shall integrate the sine of a local delay-and-sum steering angle 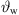 measured down from the normal plane of t, hence with negative sign, cf. Figure 1,
measured down from the normal plane of t, hence with negative sign, cf. Figure 1,
The Frenet–Serret formulas describe 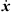 as tangential vector
as tangential vector 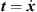 , and
, and 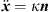 as normal vector n scaled by curvature
as normal vector n scaled by curvature 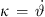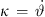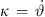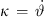 , in our case
, in our case ![$ {n}={\left[\begin{array}{ccc}\mathrm{cos}\enspace \vartheta & 0& -\mathrm{sin}\enspace \vartheta \end{array}\right]}^T,$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq24.gif) and a bi-orthogonal vector
and a bi-orthogonal vector ![$ {b}={t}\times {n}={\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}^T$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq25.gif) , so that ||t|| = ||n|| = ||b|| = 1 and t ⊥ n ⊥ b, cf. equation (2) and Figure 1.
, so that ||t|| = ||n|| = ||b|| = 1 and t ⊥ n ⊥ b, cf. equation (2) and Figure 1.
2.2 Stationary-phase approximation
At high frequencies, the integrand of equation (1) oscillates rapidly. Therefore stationary phase approximation is appropriate, which evaluates the integrand’s stationary-phase points 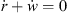 ; with derivatives abbreviated as
; with derivatives abbreviated as 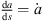 ,
, 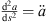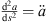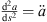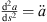 . In typical designs, there should only be a single stationary-phase point of minimum delay
. In typical designs, there should only be a single stationary-phase point of minimum delay 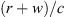 to the receiver and therefore the pressure is approximated by,
to the receiver and therefore the pressure is approximated by,
2.3 Target coverage
Our goal is to find the curvature and delay length w at each position s on the source such that the sound pressure
decays by −6β dB per doubling of distance on the listening plane that lies at zr = 0. For an equalized magnitude square, we allow a gain g and desire
2.4 Stationary-phase direction
We derive 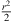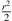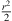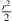 with regard to s to describe stationary-phase directions
with regard to s to describe stationary-phase directions 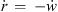 pointing from the corresponding point on the array emitting the first wave front received to the receiver on the listening plane at zr = 0,
pointing from the corresponding point on the array emitting the first wave front received to the receiver on the listening plane at zr = 0,
We use 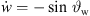 , introduce a unit-length vector
, introduce a unit-length vector 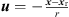 to stationary-phase receivers
to stationary-phase receivers 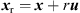 requiring
requiring 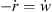 , so
, so 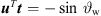 , and these stationary-phase receivers lie on a cone of local stationary-phase directions, cf. Figure 1,
, and these stationary-phase receivers lie on a cone of local stationary-phase directions, cf. Figure 1,
Below, we design the x-axis sound pressure contour at yr = 0 for receivers at zr = 0, simplifying the direction u with φw = 0 to
where the total inclination is gathered as 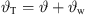 .
.
2.5 Stationary-phase magnitude
We derive 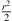 once more from equation (8) to describe
once more from equation (8) to describe 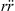 ,
,
and with 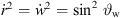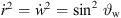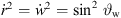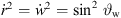 ,
, 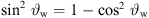 ,
, 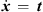 , ||t|| = 1,
, ||t|| = 1, 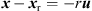 ,
, 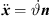 ,
, 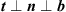 , as well as
, as well as 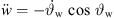 , we get a part of
, we get a part of 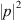 in equation (7)
in equation (7)
and hereby the equalized magnitude squared
We assume receivers at z = 0, so ![$ {\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T\left[{x}+r{u}\right]=0$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq70.gif) retrieves r by the contributions of t, n to z in equation (9)
retrieves r by the contributions of t, n to z in equation (9)
2.6 Optimum total curving
To design the sound pressure response at yr = 0, we choose φw = 0, yielding with 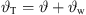
For the current positions z, total angle 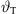 , distance r from equation (15), the required angular curvature complies with the constraint equation (7) when it becomes
, distance r from equation (15), the required angular curvature complies with the constraint equation (7) when it becomes
Its numerical integration using a phase/geometry split b, gain g2, and start inclination 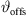 defines Algorithm 1, where S denotes the source length and N is the number of discrete elements. The total inclination
defines Algorithm 1, where S denotes the source length and N is the number of discrete elements. The total inclination 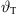 is split into geometry and delay parts by the factors a, b, linearly, and a constant inclination offset
is split into geometry and delay parts by the factors a, b, linearly, and a constant inclination offset 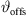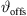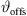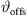 is additionally added to adjust the inclination for a straight line-source with phasing only. Geometry and phase inclination parts become
is additionally added to adjust the inclination for a straight line-source with phasing only. Geometry and phase inclination parts become
2.7 Top inclination, gain, curving split
The aiming to the audience area typically lies within 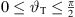 and reduces from a most horizontal aiming
and reduces from a most horizontal aiming 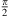 thinkable to a most upwards aiming 0 thinkable. For this reason, the total inclination decreases
thinkable to a most upwards aiming 0 thinkable. For this reason, the total inclination decreases 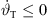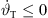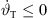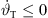 and clarifies the negative sign of
and clarifies the negative sign of 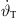 . We recognize in equation (15) that
. We recognize in equation (15) that 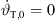 yields the loudest sound pressure
yields the loudest sound pressure
Algorithm 1. Curving of geometry and/or phase
procedure CURVING(xr,0, z0, b, β, S, N, [g2, 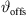 ])
])
constant:
Δs = −S/N
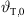 = f(xr,0, z0) ▷ according to eq. (19)
= f(xr,0, z0) ▷ according to eq. (19)
a = 1 − b ▷ to ensure a + b = 1
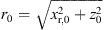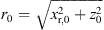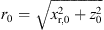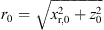 ▷ cf. Figure 2
▷ cf. Figure 2
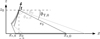 |
Figure 2 Uniform starting conditions for both curved and phased sources: top end at x0 = 0 at s = 0, inclined by |
![$ [{\vartheta }_{\mathrm{offs}}={\vartheta }_{\mathrm{T},0}]$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq96.gif) ▷ default inclination offset
▷ default inclination offset
![$ \left[{g}^2=\frac{{r}_0^{2\beta -1}}{{\mathrm{cos}}^2[b({\vartheta }_{\mathrm{T},0}-{\vartheta }_{\mathrm{offs}})}\right]$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq97.gif) ▷ default eq. (18)
▷ default eq. (18)
initialization:
w = zeros(1,N)
x = zeros(1,N)
z = zeros(1,N)
r = r0, 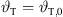 , z[1] = z0
, z[1] = z0
for n = 1...N − 1 do
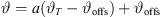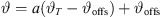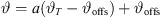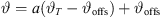 ▷ cf. eq. (17)
▷ cf. eq. (17)
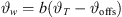 ▷ cf. eq. (17)
▷ cf. eq. (17)
x[n + 1] ← x[n] + 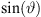 Δs ▷ num.int. (2)
Δs ▷ num.int. (2)
z[n + 1] ← z[n] + 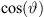 Δs ▷ num.int. (2)
Δs ▷ num.int. (2)
w[n + 1] ← w[n] − 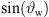 Δs ▷ num.int. (4)
Δs ▷ num.int. (4)
![$ r\leftarrow \frac{z[n]}{\mathrm{sin}\enspace {\vartheta }_{\mathrm{T}}}$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq104.gif) ▷ according to eq. (15)
▷ according to eq. (15)
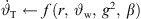 ▷ according to eq. (16)
▷ according to eq. (16)
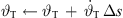 ▷ numerical integration
▷ numerical integration
end for
return w, x, z
end procedure
We need to ensure that the curvature 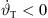 stays negative yielding a convex contour and a single stationary-phase point for each observing point as implied in equation (5). Moreover, a geometrically concave solution with
stays negative yielding a convex contour and a single stationary-phase point for each observing point as implied in equation (5). Moreover, a geometrically concave solution with 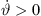 would be impractical for line-source arrays whose splay angles
would be impractical for line-source arrays whose splay angles 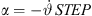 are non-negative. Choosing as a consequence both
are non-negative. Choosing as a consequence both 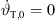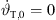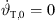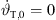 and
and 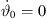 at the top of the source, the beam-steering curvature
at the top of the source, the beam-steering curvature 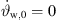 must also vanish to preserve
must also vanish to preserve 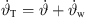 .
.
This total inclination 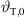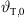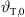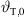 at the top of the source at x = x0 = 0 and z = z0 should be adjusted to ensure the top is the minimum-distance point supplying the remotest position xr,0 in the audience as in Figure 2,
at the top of the source at x = x0 = 0 and z = z0 should be adjusted to ensure the top is the minimum-distance point supplying the remotest position xr,0 in the audience as in Figure 2,
The top inclination is suggested to be purely geometrical 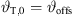 per default, so that its beam steering is neutral and broadside
per default, so that its beam steering is neutral and broadside 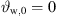 for any choice of a, b.
for any choice of a, b.
The simplest choices for a, and b are: (i) a = 1, b = 0 for a line source without phasing 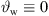 but with curving
but with curving 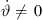 , or (ii) a = 0, b = 1 for a straight-line source without curving
, or (ii) a = 0, b = 1 for a straight-line source without curving 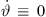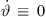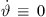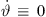 but with phasing
but with phasing 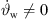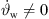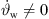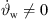 . We will also demonstrate the usefulness of mixtures in a later section, targeting the case in which multiple criteria for β should be fulfilled. For instance, the control of the curved array with equal signals fulfills the criterion β1 = 0, and
. We will also demonstrate the usefulness of mixtures in a later section, targeting the case in which multiple criteria for β should be fulfilled. For instance, the control of the curved array with equal signals fulfills the criterion β1 = 0, and 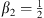 can be accomplished by additional delays.
can be accomplished by additional delays.
3 Simulation studies
In this section, the differential equation will be solved numerically as outlined in Algorithm 1. It applies stepwise updates to 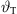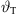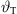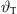 based on
based on 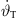 from equation (16). The algorithm’s step size Δs should be appropriately small to solve the problem accurately, by choosing a large N. In default of the optional argument g, Algorithm 1 uses equation (18) to define g2.
from equation (16). The algorithm’s step size Δs should be appropriately small to solve the problem accurately, by choosing a large N. In default of the optional argument g, Algorithm 1 uses equation (18) to define g2.
The simulations below show the result of summing individual point sources described by Green’s function positioned along the continuous source contour at 1 mm intervals. This summation is performed for frequencies ranging from 20 Hz to 20 kHz with a linear resolution of 248 points, to which and a third-octave band averaging was applied. To show broadband sound pressure curves over the listening area, results were A-weighted [32] and summarized. In addition to the A-weighted on-axis sound pressure curves, a level map of a phased line source with β = 0 demonstrates the coverage including off-axis listening positions, below. Furthermore the directivity factor is discussed, calculated as result of theoretically simplified considerations, and simulated by (delayed) point sources positioned along the desired contour.
3.1 Curved line source
For curved line sources without phasing (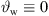 ), a = 1 and b = 0, the design equation (15) simplifies to
), a = 1 and b = 0, the design equation (15) simplifies to
and the differential equation (16) to
3.1.1 Comparison to literature
In a recent paper [28], we presented a second-order differential equation for β = 0, yielding an optimally curved arc source. While its result is perfectly equivalent for β = 0, the main difference lies in the formulation of the integration with regard to the x axis instead of the natural parameter s, which complicates generalization to β > 0 or comparison to literature. Equation (20) is shown above as it matches the classic equation obtained by Urban et al. [3], which states after re-writing the variables STEP = Δs, 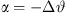 , d = r, with
, d = r, with 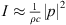 ,
,
Remarkably, equation (22) resulting from a binary Fresnel-zone-based approach only differs from stationary-phase approximation equation (20) by the missing limit Δs → 0.
A later publication [5] and variable-curvature line-source tutorials [33] chose to show a simplified relation
which is instructive and intuitively accessible. By letting 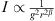 and replacing
and replacing 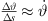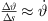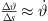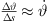 , it implies
, it implies
and hereby yields the expression
The equation demands for cabinets pointing at large distances that the splay angle between them must be small so that more cabinets radiate into the same direction. The exponent β defines the desired distance decay. Despite its easier accessibility, however, equation (25) is inaccurate compared to equation (22) whenever β → 0 gets small. While for β = 0.5 and small Δs, it makes no substantial difference which formula is used for calculation, because either 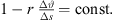 or
or 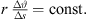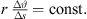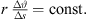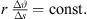 approximate
approximate 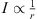 , only with a different overall gain.
, only with a different overall gain.
Without simplification, the equation (22) as defined in [3] yields upon targeting 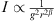 an approximation
an approximation
of equation (21), as long as STEP = Δs stays sufficiently small. In particular, the original paper used the cabinet height for STEP and the splay angles for 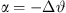 , i.e. a fixed geometric discretization determined by the hardware elements, as opposed to keeping it a free parameter adjusted for fine-enough discretization Δs → 0, when numerically solving a differential equation.
, i.e. a fixed geometric discretization determined by the hardware elements, as opposed to keeping it a free parameter adjusted for fine-enough discretization Δs → 0, when numerically solving a differential equation.
3.1.2 Curved line source: results
The differential equation of equation (21) is solved numerically by the proposed Algorithm 1 with uniform parameters xr,0 = 10 m, z0 = 2.072 m, b = 0 and source length S = 1.312 m for all decays, giving the number of discrete elements N = 1313 for a step size Δs = 1 mm. Equation (19) specifies the total inclination on top of the source 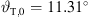 and for β = 0, the gain parameter is calculated by equation (18) yielding a value of
and for β = 0, the gain parameter is calculated by equation (18) yielding a value of 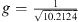 . For the other decay values, g was set manually to g = 0.443 for β = 0.25 and g = 0.599 for β = 0.5, in order to supply the same listening positions 0 ≤ xr ≤ 10 m with unchanged source length S.
. For the other decay values, g was set manually to g = 0.443 for β = 0.25 and g = 0.599 for β = 0.5, in order to supply the same listening positions 0 ≤ xr ≤ 10 m with unchanged source length S.
Figure 3 shows the source contour for different decays and Figure 4 the resulting A-weighted sound pressure profiles with dB offsets to make the β = {0, 0.25, 0.5} curves to go through {0, −3.5, −7} dB at the distance of xr = 4 m. The levels do not follow the theoretical roll-off curves −6β dB per doubling of the distance beyond xr > 7 m as stationary phase approximation assumes an infinite line integral although the actual length is finite.
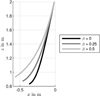 |
Figure 3 Curved line source contours for different decays β. |
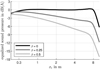 |
Figure 4 A-weighted sound pressure levels of curved line sources for different decays β with mixed x-axis scaling, linear for xr ≤ 1 and logarithmic for xr > 1, with the target range 0 ≤ xr ≤ 10 m. |
Another parameter to be considered for radiation characteristics is the directivity factor Q. Figure 5 shows the directivity index DI = 10 lg Q for both cases, curved and phased line source with different decays β. The radiation of the source was calculated at 10 m distance as summation of individual point sources with Δs = 1 mm. For low frequencies, omnidirectional radiation is seen, which coincides with theoretical considerations for frequencies below 130 Hz (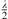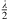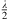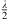 ). At frequencies above 500 Hz, the curves for different decay values differ, with small decay values leading to higher directivity. With
). At frequencies above 500 Hz, the curves for different decay values differ, with small decay values leading to higher directivity. With 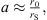 Sections A.3 and A.4 we find
Sections A.3 and A.4 we find
The results are shown as dotted lines in Figure 5 and show the same trends as the simulated solid lines, where a = 7 corresponds to the ratio of distances, within which the level curves fulfill the decay profile, cf. Figure 4. The horizontal extent Δx is 9.83 cm for β = 0, it is 19.82 cm for β = 0.25, and 32.14 cm for β = 0.5.
 |
Figure 5 Directivity index for curved (thin) and phased (bold) line sources with different decays β compared to equation (27) (dotted). |
 |
Figure 6 Discretization of a continuously curved line source (A) according to the β = 0 example from Figure 3 to: a polygon of straight-line sources with splay angles rounded to integer degrees (B) and gaps between these straight-line segments (C); graphs are rotated by |
Professional line-source array systems typically contain multi-way transducers, of which the larger layout of the low- and mid-frequency transducers is horizontally directional, instead of radiating axisymmetrically. Similarly, their vertical high frequency line-source transducers, e.g. f > 1 kHz, are typically equipped with horizontal waveguides or wedge-shaped horns that limit horizontal radiation to 110°, so roughly a third of the 360° panorama, or to 70° which is roughly its fifth. The modeled DI can be adapted correspondingly with an increase by +5 dB for 110° or +7 dB for 70° horizontal coverage.
3.1.3 Discretization of source and splay angles
Later we will use a prototype of a line array to show the effectiveness of the formalism in practice. Since is solved with the same parameters as in Section 3.1.2 and the resulting continuous source is then composed by point sources that are positioned along the contour, cf. Figure 7A. To simulate a practical device built from discrete elements, the contour was discretized into a polygon of 8.2 cm straight-line segments in Figure 7B. The splay angles are chosen so that the error made in the total inclination caused by using integer ° values for the splay angles is kept minimal. The same procedure is executed for Figure 7C but with shorter 6.2 cm straight-line segments with the same splay angles but leaving gaps in between. Due to discretization with integer-degrees splay angles, the lost control of small curvatures yields a boost of the sound pressure level between 7 m and 8 m for β = 0 in our example, cf. Figure 7. Gaps between the straight-line source elements weaken the attenuation of spatial aliasing. It occurs at frequencies above 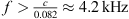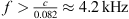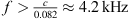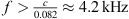 where the inter-element spacing exceed a wavelength, which causes a noticeable downwards leakage of sound to listeners at xr < 3 m with broadside steering
where the inter-element spacing exceed a wavelength, which causes a noticeable downwards leakage of sound to listeners at xr < 3 m with broadside steering 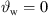 .
.
 |
Figure 7 A-weighted sound pressure level for different decays β and different discretization with mixed x-axis scaling, linear for xr ≤ 1 and logarithmic for xr > 1, as above; continuous line source (dotted), discrete point sources with 8.2 cm (dashed), straight 6.2 cm line-sources at the same spacing with inclination increments rounded to integer ° values (solid). |
 |
Figure 8 Simulated A weighted sound pressure map of a phased line source for β = 0 over a listening area of 10 m × 10 m. |
 |
Figure 9 A-weighted sound pressure levels of a phased source with different decays β for a target range 0 ≤ xr ≤ 10 m, with a continuous source Figure 6A or discrete segments Figure 6C of integer sample delays (48 kHz sample rate); the x-axis is scaled linearly for xr ≤ 1 and logarithmically for xr > 1. |
3.2 Phased straight-line source
With a = 0, we get the differential equation for the beamforming angle of a straight-line source from equation (16),
3.2.1 Phased straight-line source: results
The differential equation (28) is solved numerically by Algorithm 1 with uniform parameters xr,0 = 10 m, z0 = 2.117 m, b = 1, 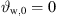 and source length S = 1.312 m for all decay values, resulting in the number of discrete elements N = 1313 for a step size Δs = 1 mm. Equation (19) defines the inclination on top of the source
and source length S = 1.312 m for all decay values, resulting in the number of discrete elements N = 1313 for a step size Δs = 1 mm. Equation (19) defines the inclination on top of the source 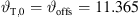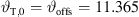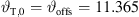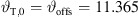 ° and for β = 0, the gain parameter is calculated by equation (18) yielding a value of
° and for β = 0, the gain parameter is calculated by equation (18) yielding a value of 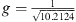 . For the other decay values, g was set manually, g = 0.449 for β = 0.25 and g = 0.614 for β = 0.5. Figure 10 shows the delay lengths for different decay values, and Figure 9 describes the resulting A-weighted sound pressure curves for a continuously phased source (dotted lines) compared to direct sound pressures curves of a discrete phased source with enclosure height 8.2 cm, gaps in between and rounded delays being accurate to 1 sample at fs = 48 kHz. The SPL plots for the continuous source exhibit the same trend as those for the purely curved source. For very close listening positions, the curves differ due to discretization and spatial aliasing. The delays also cause a comb filter, which is greatest at β = 0 due to the temporal structure of the summed impulse response and has the opposite effect to spatial aliasing. The A-weighted sound pressure for β = 0 including off-axis listening positions can be found as a level map in Figure 8 over a 10 m × 10 m listening area. The coverage for which level changes stays below 1 dB reaches a limit of |φw| = 27.5° for closer observation points. For farther observation points (5 m < xr < 7.8 m) the coverage gets wider up to maximum of |φw| = 35° for r = 8.5 m.
. For the other decay values, g was set manually, g = 0.449 for β = 0.25 and g = 0.614 for β = 0.5. Figure 10 shows the delay lengths for different decay values, and Figure 9 describes the resulting A-weighted sound pressure curves for a continuously phased source (dotted lines) compared to direct sound pressures curves of a discrete phased source with enclosure height 8.2 cm, gaps in between and rounded delays being accurate to 1 sample at fs = 48 kHz. The SPL plots for the continuous source exhibit the same trend as those for the purely curved source. For very close listening positions, the curves differ due to discretization and spatial aliasing. The delays also cause a comb filter, which is greatest at β = 0 due to the temporal structure of the summed impulse response and has the opposite effect to spatial aliasing. The A-weighted sound pressure for β = 0 including off-axis listening positions can be found as a level map in Figure 8 over a 10 m × 10 m listening area. The coverage for which level changes stays below 1 dB reaches a limit of |φw| = 27.5° for closer observation points. For farther observation points (5 m < xr < 7.8 m) the coverage gets wider up to maximum of |φw| = 35° for r = 8.5 m.
 |
Figure 10 Delay length w for different decays β. |
3.2.2 Comparison to literature
Electronically steered line arrays for sound reinforcement can be found in literature, however not fixed to using delays, only. Meyer [14, 34] employs individual filters to control each array loudspeaker and proposes to mount the line arrays along the ceiling. Different designs are used with regard to the arrays’ throw distance, short-throw vs. long-throw array, and to keep the direct sound coverage of the audience flat. Van der Werff [15] discusses wall-mounted line arrays with non-uniformly spaced transducers, as nested array, with individual filtering with IIR low-pass filter designs. The goal of his work is to increase the direct-to-reverberant ratio in large halls by achieving a flat direct sound pressure level profile of 0 dB per distance doubling, and the design was verified in EASE 1.2. And finally, Duran Audio’s Digital Directivity Synthesis is a well-known DSP-assisted method based on least-squares for uniformly spaced line arrays [11]. Its optimization of the desired direct sound pressure level profiles takes transducer directivity into account. The method requires the implementation of FIR filters as signal processing done for each loudspeaker.
Algorithm 2. Two-target curving of geometry and phase
procedure TWOBETA(xr,0, z0, β1, β2, S, N, 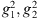 ,
, 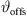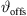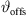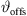 )
)
constant:
Δs = −S/N
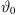 = f(xr,0, z0) ▷ according to eq. (19)
= f(xr,0, z0) ▷ according to eq. (19)
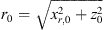 ▷ cf. Figure 2
▷ cf. Figure 2
initialization:
w = zeros(1,N)
x = zeros(1,N)
z = zeros(1,N)
r1 = r2 = r0, ![$ \vartheta [1]={\vartheta }_0$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq173.gif) , z[1] = z0
, z[1] = z0
for n = 1...N − 1 do
w[n + 1] ← w[n] − 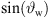 Δs ▷ num.int. (4)
Δs ▷ num.int. (4)
x[n + 1] ← x[n] + 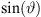 Δs ▷ num.int. (2)
Δs ▷ num.int. (2)
z[n + 1] ← z[n] + 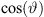 Δs ▷ num.int. (2)
Δs ▷ num.int. (2)
![$ {r}_1\leftarrow \frac{z[n]}{\mathrm{sin}\enspace \vartheta },\enspace \hspace{1em}{r}_2\leftarrow \frac{z[n]}{\mathrm{sin}(\vartheta +{\vartheta }_{\mathrm{w}})}$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq177.gif) ▷ cf. eq. (15)
▷ cf. eq. (15)
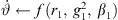 ▷ according to eq. (21)
▷ according to eq. (21)
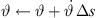 ▷ numerical integration
▷ numerical integration
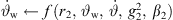 ▷ acc. to eq. (29)
▷ acc. to eq. (29)
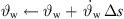 ▷ numerical integration
▷ numerical integration
end for
return w, x, z
end procedure
3.3 Curved and phased line source
To support two simultaneous coverage designs (preserving mixing-balance and envelopment) for a large audience area, phasing delays are used in combination with geometrical curving. In addition to a decay β1 accomplished by driving the cabinets of a curved array with identical signals, delays between individually driven cabinets can be used to satisfy an alternative decay β2.
First, equation (21) is solved for a purely curved source (b = 0) with β1 as shown in Algorithm 1, and afterwards the required delay lengths for another choice of β2 is calculated preserving the geometrical curvature 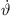 ,
,
which is summarized in Algorithm 2.
As this design and algorithm will be analyzed in measurements using prototypical hardware in the next section, graphical analysis of the results will be shown below.
4 Experimental setup
To show the effectiveness of the formalism in practice, the reproducible miniature line array presented in [35] was used, cf. Figure 11. The trapezoidal shape was chosen so that a maximum tilt angle of 10 degrees can be set. SB Acoustics SB65WBAC25-4 were used as the 2.5-inch full-range speakers.
 |
Figure 11 Miniature Line Array of eight 3D printed enclosures (closed 0.4 l boxes). |
For the measurements, 12 enclosures are lined up for which we obtain the continuous source contour and delay lengths from Algorithm 1. The measurements took place in an auditorium (30 m × 9 m × 3.5 m) with a reverberation time of T60 ≈ 0.82 s. To focus on verifying the direct sound design, the impulse responses were truncated to the first 300 samples (6.25 ms at fs = 48 kHz). The gain values g for β = 0 are calculated by equation (18), for the other decay values g was set manually, g = 0.46 for β = 0.25 and g = 0.65 for β = 0.5. The solution is then discretized using a step size of 8.2 cm which corresponds to the distance between two neighbouring drivers. In order to record the position-dependent direct sound pressure level curves, impulse responses were measured along 20 positions (on-axis) starting at xr = 1 m and ending at xr = 10.5 m. Pressure zone microphones were positioned on the ground to avoid floor reflections in the measurements. We applied equalization to obtain a flat frequency response between 200 Hz and 20 kHz for the single array element. Moreover, a filter with magnitude increasing by 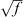 until the spatial aliasing frequency was employed to equalize the otherwise pink sound pressure of a linear arrangement of ideal point sources, cf. equation (7). The results are averaged in third octaves and the curves are plotted as A-weighted sum.
until the spatial aliasing frequency was employed to equalize the otherwise pink sound pressure of a linear arrangement of ideal point sources, cf. equation (7). The results are averaged in third octaves and the curves are plotted as A-weighted sum.
4.1 Curved line source
Figure 12 shows the A weighted sum over distance (on-axis) for different decays β compared to the simulated curves with the same discretization as in Figure 6C. The measured results show almost identical curves to the simulation and the artefacts caused by discretization of source and splay angles are observed.
 |
Figure 12 A-weighted measured sound pressure of curved arrays (solid) with different decays over distance compared to the simulated discretized source (dashed) with rounded splay angles keeping the error made in total inclination minimal. |
 |
Figure 13 Measured A weighted sound pressure map of a phased array with β = 0 compared to simulated contours in steps of 1 dB (dashed). |
4.2 Phased line source
Figure 14 shows the A-weighted on-axis sound pressure curves in comparison to the simulated for different decays β. Also here, the measured results follow almost the theoretical simulated based on point source summation. The noticeable differences are close to the source where the beamforming no longer reaches closer listening positions and spatial aliasing affects the results. Figure 13 presents the measured coverage (solid) including off-axis listening positions of a phased array with β = 0 compared to the simulated (dashed). We observe a lower sound pressure for lateral listening positions because the linearly arranged point sources in the simulation do not take the horizontal directivity of the drivers into account.
 |
Figure 14 A-weighted measured sound pressure of phased arrays (solid) with different decays over distance compared to the simulated discretized source (dashed) with rounded delays at fs = 48 kHz. |
4.3 Mixed curve and phase design
For the mixed design, we take the curved line source from Section 4.1 with β1 = 0 and use the corresponding time of flight to satisfy β2 = 0.5 according to Algorithm 2. The rounded delays at fs = 48 kHz were inserted in the off-line analysis. Figure 15 shows the A-weighted sound pressure profile of a purely curved source with β = 0 and compares the A-weighted profile of a curved line source with β = 0.5 with the curve of the mixed design.
 |
Figure 15 A-weighted measured sound pressure of curved arrays (solid) with decays β = 0 and β = 0.5 and mixed array with β1 = 0 and β2 = 0.5 over distance compared to simulated discretized sources (dashed). |
The profile for a purely curved source and the one of the mixed design differ in the vicinity of the source only, because the impulse responses of the enclosures differ in time structure in this area, yielding a different sum. Nevertheless, both follow the simulated −3 dB per doubling of distance.
5 Conclusion
This paper presented design equations for continuously curved and phased line sources with the target to accomplish desired sound pressure roll-offs. The stationary phase approximation was applied to the contour integral of a Green’s function with delay (phasing) to obtain a second-order nonlinear differential equation for curving and phasing. The discretized results are directly applicable to design curvature and phasing of discrete line source arrays. Simulations of the continuous source based on summation of point sources positioned along the line source contour showed the ideal −6β dB profiles per doubling of the distance. Furthermore, the simulations revealed the effects caused by the discretization of the source. The theoretical results were underlined by measurements of a line array prototype. Moreover, the results showed that a two-target design based on curving and phasing is feasible.
Future work should consider psychoacoustic evaluations of line sources with different β profiles for medium-sized immersive sound reinforcement for 50–250 listeners to assess improvements in envelopment and direct-sound mix. Experiments should also take frequency-response homogeneity into account, which is often optimized as a trade-off with the coverage parameter β, see also [33].
Acknowledgments
Our research was funded by the Austrian Science Fund (FWF): P 35254-N, Envelopment in Immersive Sound Reinforcement (EnImSo). The authors thank Thomas Musil for his design improvements on our miniature line array.
Conflict of interests
The authors declared no conflicts of interests.
Data Availability Statement
The research data associated with this article are included in the supplementary material of this article [36].
Appendix
A.1 Line array near field
When observing a line source of the length S at the normal distance r to one of its ends, the distance to its other end is 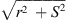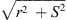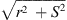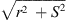 . A distance difference
. A distance difference 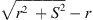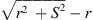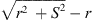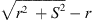 to both ends that may exceed a
to both ends that may exceed a 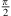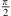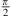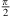 phase shift towards r → 0 defines the acoustic near field, within which the distance decay can differ from
phase shift towards r → 0 defines the acoustic near field, within which the distance decay can differ from 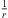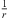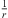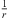 , with
, with 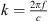 and
and 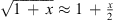 ,
,
Example: The near field extends to 10 m for a source of the length 1 m at a frequency of f = 5c = 1.7 kHz.
A.2 Line array aliasing
A line array composed of discrete elements of the height and spacing h driven in phase radiates waves focused to directions perpendicular to the line. It exhibits uncontrolled radiation due to spatial aliasing at and above the frequency at which also waves propagating along the line fit the in-phase control,
Example: The frequency should stay below 3 kHz for 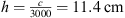 to avoid spatial aliasing.
to avoid spatial aliasing.
A.3 Directivity index of a line source
For very low frequencies f → 0, any phased/curved line source has vanishing extent in terms of wavelengths and the directivity index is zero DI → 0 dB.
Any phased/curved line source exhibits a length S as its larger geometric extent. Its directivity index first rises when the length S exceeds half a wavelength 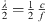
Around this frequency, the directivity function is well approximated by a line source of the length S, with 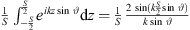 . The directivity factor of an axisymmetric radiation is 2 divided by the squared directivity pattern integrated along the inclination d sin ϑ,
. The directivity factor of an axisymmetric radiation is 2 divided by the squared directivity pattern integrated along the inclination d sin ϑ,
and at low frequencies we approximate the sine integral Si(kS) by kS and cosine cos(kS) by 1, yielding Q ≈ 1, and the asymptotic value of Si(kS) is 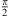 at high frequencies, where we may neglect cos(kS) + 1 and get
at high frequencies, where we may neglect cos(kS) + 1 and get 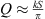 , or in total
, or in total
After the linear increase of the directivity factor above 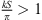 , a slight saturation will be reached when the second extent of the curved/phased line source
, a slight saturation will be reached when the second extent of the curved/phased line source 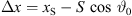 or Δx = wS exceeds half a wavelength
or Δx = wS exceeds half a wavelength
which is conveniently denoted as frequency f1 scaled by the approximate aspect ratio 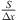 of the source.
of the source.
A.4 Directivity index of a directional point source with predefined coverage
To estimate the directivity index, we consider the far-field sound pressure of a directional point source,
mounted at the height z0 above the audience and exhibiting a roughly axisymmetric directivity function g around the vertical axis. Listeners at ear height are reached if the distance r relates to the variable inclination angle by
and a correspondingly re-formulated directivity factor depending on this r can be tailored so that listeners receive
and hereby a well-controlled direct-sound level decaying with −6β dB per doubling of the distance. To avoid radiation to angles outside 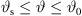 , the directivity function must vanish elsewhere, accordingly, and we may substitute
, the directivity function must vanish elsewhere, accordingly, and we may substitute 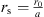 and choose rs = z0 for simplicity,
and choose rs = z0 for simplicity,
The characterization of a directivity pattern relies on observation at a direction-independent distance, e.g. r0, but we may keep r as unrelated variable defining the directivity function g by the angle-dependent distance to the listeners,
With the directivity pattern integrated along the inclination 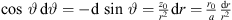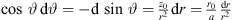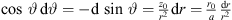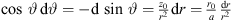 the directivity factor of the axisymmetric radiation is
the directivity factor of the axisymmetric radiation is
For curved/phased line-source arrays, this rough asymptotic approximation can be assumed to hold for high frequencies f > f2, where the directivity function vanishes outside the angular range 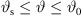 .
.
References
- W. Ahnert, D. Noy: Sound reinforcement for audio engineers, Taylor & Francis Ltd, 2023. [Google Scholar]
- C. Heil, M. Urban, Sound fields radiated by multiple sound sources arrays, in: 92nd AES Conv, Vienna, 1992. [Google Scholar]
- M. Urban, C. Heil, P. Bauman: Wavefront sculpture technology. Journal of the Audio Engineering Society 51, 10 (2003) 912–932. [Google Scholar]
- F. Straube, F. Schultz, M. Makarski, S. Spors, S. Weinzierl: Evaluation strategies for the optimization of line source arrays, in: 59th AES Conf, Montreal, Canada, 2015. [Google Scholar]
- F. Straube, F. Schultz, D.A. Bonillo, S. Weinzierl: An analytical approach for optimizing the curving of line source arrays. Journal of the Audio Engineering Society 66, 1/2 (2018) 4–20. [CrossRef] [Google Scholar]
- A. Hölter, F. Straube, F. Schultz, S. Weinzierl: Enhanced polygonal audience line curving for line source arrays, in: 150th AES Convention, 2021. [Google Scholar]
- A. Thompson: Line array splay angle optimisation, in: Reproduced Sound 22 Conference, Oxford, 2006. [Google Scholar]
- A. Thompson, Improved methods for controlling touring loudspeaker arrays, in: 127th AES Convention, New York, USA, 2009. [Google Scholar]
- A. Thompson, J. Baird, B. Webb, Numerically optimized touring loudspeaker arrays – practical applications, in: 131st AES Convention, New York, USA, 2011. [Google Scholar]
- F. Toole, Sound Reproduction: Loudspeakers and Rooms, in: Audio Engineering Society Presents Series, Elsevier, 2008. [Google Scholar]
- G. van Beuningen, E. Start: Optimizing directivity properties of DSP controlled loudspeaker arrays, in: Reproduced Sound 16 Conference, Stratford upon Avon, 2000. [Google Scholar]
- D. Ward, R. Kennedy, R. Williamson: Constant directivity beamforming, in: Microphone Arrays, Springer, Berlin, Heidelberg, 2001, pp. 3–17. [CrossRef] [Google Scholar]
- M. Goodwin, G. Elko: Constant beamwidth beamforming, in: IEEE ICASSP, Vol. 1, Minneapolis, USA, 1993, pp. 169–172. [CrossRef] [Google Scholar]
- D.G. Meyer: Digital control of loudspeaker array directivity. Journal of the Audio Engineering Society 32, 10 (1984) 747–754. [Google Scholar]
- J. van der Werff, Design and implementation of a sound column with exceptional properties, in: 96th AES Convention, Amsterdam, Netherlands, 1994. [Google Scholar]
- R. Mailloux: Phased array antenna handbook, 3rd edn., Artech House, 2017. [Google Scholar]
- T. Taylor: Design of line-source antennas for narrow beamwidth and low side lobes. Transactions of the IRE Professional Group on Antennas and Propagation 3, 1 (1955) 16–28. [CrossRef] [Google Scholar]
- P. McManamon, T. Dorschner, D. Corkum, L. Friedman, D. Hobbs, M. Holz, S. Liberman, H. Nguyen, D. Resler, R. Sharp, E. Watson: Optical phased array technology. Proceedings of the IEEE, 84, 2 (1996) 268–298. [CrossRef] [Google Scholar]
- H. Shanks: A geometrical optics method of pattern synthesis for linear arrays. IRE Transactions on Antennas and Propagation 8, 5 (1960) 485–490. [CrossRef] [Google Scholar]
- B. Chiang, D.H.-S. Cheng: Curvilinear arrays. Radio Science 3, 5 (1968) 405–409. [CrossRef] [Google Scholar]
- A. Chakraborty, B. Das, G. Sanyal: Determination of phase functions for a desired onedimensional pattern. IEEE Transactions on Antennas and Propagation 29, 3 (1981) 502–506. [CrossRef] [Google Scholar]
- E. Start: Direct sound enhancement by wavefield synthesis. Ph.D. dissertation Technical University Delft, 1997. [Google Scholar]
- G. Firtha: A generalized wave field synthesis framework with application for moving virtual sources. Ph.D. dissertation Budapest University of Technologies and Economics, 2019. [Google Scholar]
- P. Grandjean, A. Berry, P.-A. Gauthier: Sound field reproduction by combination of circular and spherical higher-order ambisonics: part I — a new 2.5-d driving function for circular arrays. Journal of Audio Engineering Society 69, 3 (2021) 152–165. [CrossRef] [Google Scholar]
- F. Schultz: Sound field synthesis for line source array applications in large-scale sound reinforcement. Ph.D. dissertation University of Rostock, 2016. [Google Scholar]
- SMPTE RP 2096–1:2017, Recommended practice – cinema sound system baseline setup and calibration, 2017. [Google Scholar]
- J. Nettingsmeier, D. Dohrmann: Preliminary studies on large-scale higher-order ambisonic sound reinforcement systems, in: Ambisonics Symposium, Lexington, KY, 2011. [Google Scholar]
- L. Gölles, F. Zotter: Optimally curved arc source for sound reinforcement, in: Fortschritte der Akustik, DAGA, Vienna, 2021. [Google Scholar]
- F. Zotter, S. Riedel, L. Gölles, M. Frank: Acceptable imbalance of sound-object levels for off-center listeners in immersive sound reinforcement, in: Fortschritte der Akustik, DAGA, Hamburg, 2023. [Google Scholar]
- S. Riedel, F. Zotter: Surrounding line sources optimally reproduce diffuse envelopment at offcenter listening positions JASA Express Letters 2, 9 (2022) 094404. [CrossRef] [PubMed] [Google Scholar]
- S. Riedel, L. Gölles, F. Zotter, M. Frank: Modeling the listening area of envelopment, in: Fortschritte der Akustik, DAGA, Hamburg, 2023. [Google Scholar]
- ÖVE/ÖNORM EN 61672–1: Electroacoustics – Sound level meters – Part 1: Specifications, OVE/Austrian Standards Institute, Vienna, AT, Standard, 2015. [Google Scholar]
- F. Montignies: Understanding line source behaviour – for better optimization, in: VCLS Tutorial, AES, 2020. [Google Scholar]
- D.G. Meyer: Multiple-beam, electronically steered line-source arrays for sound-reinforcement applications. Journal of the Audio Engineering Society 38, 4 (1990) 237–249. [Google Scholar]
- L. Gölles, F. Zotter, L. Merkel: Miniature line array for immersive sound reinforcement, in: Proceedings of AES SIA Conf., Huddersfield, 2023. [Google Scholar]
- L. Gölles and F. Zotter: Supplementary material for theory of continuously curved and phased line sources for sound reinforcement. [Online]. Available at https://phaidra.kug.ac.at/o:129841. [Google Scholar]
Cite this article as: Gölles L. & Zotter F. 2023. Theory of continuously curved and phased line sources for sound reinforcement. Acta Acustica, 7, 52.
All Figures
 |
Figure 1 Continuous arc-shaped source (solid grey) with accompanying Frenet trihedron (top) at the point |
| In the text | |
 |
Figure 2 Uniform starting conditions for both curved and phased sources: top end at x0 = 0 at s = 0, inclined by |
| In the text | |
 |
Figure 3 Curved line source contours for different decays β. |
| In the text | |
 |
Figure 4 A-weighted sound pressure levels of curved line sources for different decays β with mixed x-axis scaling, linear for xr ≤ 1 and logarithmic for xr > 1, with the target range 0 ≤ xr ≤ 10 m. |
| In the text | |
 |
Figure 5 Directivity index for curved (thin) and phased (bold) line sources with different decays β compared to equation (27) (dotted). |
| In the text | |
 |
Figure 6 Discretization of a continuously curved line source (A) according to the β = 0 example from Figure 3 to: a polygon of straight-line sources with splay angles rounded to integer degrees (B) and gaps between these straight-line segments (C); graphs are rotated by |
| In the text | |
 |
Figure 7 A-weighted sound pressure level for different decays β and different discretization with mixed x-axis scaling, linear for xr ≤ 1 and logarithmic for xr > 1, as above; continuous line source (dotted), discrete point sources with 8.2 cm (dashed), straight 6.2 cm line-sources at the same spacing with inclination increments rounded to integer ° values (solid). |
| In the text | |
 |
Figure 8 Simulated A weighted sound pressure map of a phased line source for β = 0 over a listening area of 10 m × 10 m. |
| In the text | |
 |
Figure 9 A-weighted sound pressure levels of a phased source with different decays β for a target range 0 ≤ xr ≤ 10 m, with a continuous source Figure 6A or discrete segments Figure 6C of integer sample delays (48 kHz sample rate); the x-axis is scaled linearly for xr ≤ 1 and logarithmically for xr > 1. |
| In the text | |
 |
Figure 10 Delay length w for different decays β. |
| In the text | |
 |
Figure 11 Miniature Line Array of eight 3D printed enclosures (closed 0.4 l boxes). |
| In the text | |
 |
Figure 12 A-weighted measured sound pressure of curved arrays (solid) with different decays over distance compared to the simulated discretized source (dashed) with rounded splay angles keeping the error made in total inclination minimal. |
| In the text | |
 |
Figure 13 Measured A weighted sound pressure map of a phased array with β = 0 compared to simulated contours in steps of 1 dB (dashed). |
| In the text | |
 |
Figure 14 A-weighted measured sound pressure of phased arrays (solid) with different decays over distance compared to the simulated discretized source (dashed) with rounded delays at fs = 48 kHz. |
| In the text | |
 |
Figure 15 A-weighted measured sound pressure of curved arrays (solid) with decays β = 0 and β = 0.5 and mixed array with β1 = 0 and β2 = 0.5 over distance compared to simulated discretized sources (dashed). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



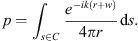
![$$ {x}={\int }_0^{\mathrm{s}}{t}\enspace \mathrm{d}s+{{x}}_0,\enspace \hspace{1em}\hspace{1em}{t}={\left[\begin{array}{ccc}\mathrm{sin}\enspace \vartheta & 0& \mathrm{cos}\enspace \vartheta \end{array}\right]}^T, $$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq12.gif)
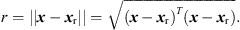
![$ {x}(s)\enspace ={\left[\begin{array}{ccc}x(s)& 0& z(s)\end{array}\right]}^T,$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq233.gif)
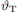
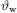
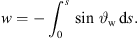
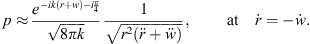
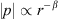
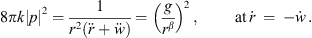
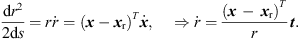
![$$ {u}=-{t}\enspace \mathrm{sin}\enspace {\vartheta }_{\mathrm{w}}+{n}\enspace \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{cos}\enspace {\phi }_{\mathrm{w}}+{b}\enspace \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{sin}\enspace {\phi }_{\mathrm{w}}=\left[\begin{array}{c}-\mathrm{sin}\enspace \vartheta \enspace \mathrm{sin}\enspace {\vartheta }_{\mathrm{w}}+\mathrm{cos}\enspace \vartheta \enspace \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{cos}\enspace {\phi }_{\mathrm{w}}\\ \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{sin}\enspace {\phi }_{\mathrm{w}}\\ -\mathrm{cos}\enspace \vartheta \enspace \mathrm{sin}\enspace {\vartheta }_{\mathrm{w}}-\mathrm{sin}\enspace \vartheta \enspace \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{cos}\enspace {\phi }_{\mathrm{w}}\end{array}\right]. $$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq49.gif)
![$$ {u}{|}_{{\phi }_{\mathrm{w}}=0}=\left[\begin{array}{c}\mathrm{cos}(\vartheta +{\vartheta }_{\mathrm{w}})\\ 0\\ \mathrm{sin}(\vartheta +{\vartheta }_{\mathrm{w}})\end{array}\right], $$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq51.gif)
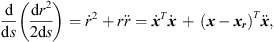
![$$ r\left(\ddot{r}+\ddot{w}\right)={\parallel {t}\parallel }^2\enspace -{\dot{r}}^2+r\stackrel{\dot }{\vartheta }\enspace {{u}}^T{n}+r\enspace \ddot{w}=1-\left[1-{\mathrm{cos}}^2\enspace {\vartheta }_{\mathrm{w}}\right]-r\stackrel{\dot }{\vartheta }\enspace \mathrm{cos}\enspace {\vartheta }_{\mathrm{w}}\enspace \mathrm{cos}\enspace {\phi }_{\mathrm{w}}-r{\stackrel{\dot }{\vartheta }}_{\mathrm{w}}\enspace \mathrm{cos}{\enspace \vartheta }_{\mathrm{w}}, $$](/articles/aacus/full_html/2023/01/aacus230050/aacus230050-eq66.gif)