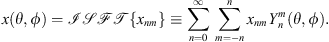| Issue |
Acta Acust.
Volume 6, 2022
Topical Issue - Auditory models: from binaural processing to multimodal cognition
|
|
|---|---|---|
| Article Number | 4 | |
| Number of page(s) | 18 | |
| DOI | https://doi.org/10.1051/aacus/2021055 | |
| Published online | 26 January 2022 | |
Scientific Article
Assessing HRTF preprocessing methods for Ambisonics rendering through perceptual models
Imperial College London, London SW7 2AZ, United Kingdom
* Corresponding author: isaac.engel@imperial.ac.uk
Received:
29
March
2021
Accepted:
9
December
2021
Binaural rendering of Ambisonics signals is a common way to reproduce spatial audio content. Processing Ambisonics signals at low spatial orders is desirable in order to reduce complexity, although it may degrade the perceived quality, in part due to the mismatch that occurs when a low-order Ambisonics signal is paired with a spatially dense head-related transfer function (HRTF). In order to alleviate this issue, the HRTF may be preprocessed so its spatial order is reduced. Several preprocessing methods have been proposed, but they have not been thoroughly compared yet. In this study, nine HRTF preprocessing methods were used to render anechoic binaural signals from Ambisonics representations of orders 1 to 44, and these were compared through perceptual hearing models in terms of localisation performance, externalisation and speech reception. This assessment was supported by numerical analyses of HRTF interpolation errors, interaural differences, perceptually-relevant spectral differences, and loudness stability. Models predicted that the binaural renderings’ accuracy increased with spatial order, as expected. A notable effect of the preprocessing method was observed: whereas all methods performed similarly at the highest spatial orders, some were considerably better at lower orders. A newly proposed method, BiMagLS, displayed the best performance overall and is recommended for the rendering of bilateral Ambisonics signals. The results, which were in line with previous literature, indirectly validate the perceptual models’ ability to predict listeners’ responses in a consistent and explicable manner.
Key words: Binaural models / Ambisonics / HRTF preprocessing / Spatial audio / Binaural rendering
© I. Engel et al., Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
1.1 Binaural rendering and Ambisonics
Binaural rendering allows to present auditory scenes through headphones while preserving spatial cues, so the listener perceives the simulated sound sources at precise locations outside their head [1]. Traditionally, this is achieved by convolving an anechoic audio signal with a head-related impulse response (HRIR) [2]. Typically, HRIRs are measured or simulated for a set of directions on a specific listener in anechoic conditions. Convolving signals with HRIRs is a convenient method to simulate a limited number of sound sources in an anechoic environment, but it cannot be easily used to accurately render reverberation or “scene-based” spatial audio formats, e.g. recorded with spherical microphone arrays. Furthermore, the implementation of rotations, in order to allow the listeners to turn their head and keep the sources fixed relative to the surrounding space, can be relatively inconvenient when using HRIRs. For such applications and features, it is common to employ Ambisonics instead.
Ambisonics, first introduced by Gerzon [3], is an audio signal processing framework that allows to conveniently record, represent, post-process and reproduce spatial audio [4]. Although it was initially intended for loudspeaker playback, Ambisonics has recently found a niche in binaural (i.e. headphone-based) audio reproduction, mostly due to an increased interest in virtual reality (VR) and augmented reality (AR). For instance, the framework has recently found use in VR-focused acoustic simulation engines by Facebook (formerly Oculus) [5] and Google [6].
In essence, Ambisonics allows to “encode” a three-dimensional sound field by projecting it on a hypothetical sphere surrounding the listener. Under this representation, the signal can be conveniently manipulated through a mathematical framework known as spherical harmonics (SH) – an excellent introduction for its usage in acoustics is given in Rafaely’s book ([7], Chap. 2). When a sound field is encoded into the Ambisonics domain, it is assigned an inherent spatial order ( ), also known as truncation order, which dictates its spatial resolution. As a general rule, lower orders offer a coarser spatial resolution, leading to an increased width or “blurryness” of rendered sound sources, while higher orders offer finer resolution, leading to narrower and better-localised sources [8]. The spatial order of an Ambisonics signal is often constrained by the application, e.g. commercial microphone arrays typically operate at order 4 or lower, while real-time acoustic simulations benefit from working with low orders, as it reduces computational costs [5].
), also known as truncation order, which dictates its spatial resolution. As a general rule, lower orders offer a coarser spatial resolution, leading to an increased width or “blurryness” of rendered sound sources, while higher orders offer finer resolution, leading to narrower and better-localised sources [8]. The spatial order of an Ambisonics signal is often constrained by the application, e.g. commercial microphone arrays typically operate at order 4 or lower, while real-time acoustic simulations benefit from working with low orders, as it reduces computational costs [5].
For binaural playback, an Ambisonics signal must be “decoded” to two channels (left and right ears) by pairing it with a head-related transfer function (HRTF), which is how we refer to an HRIR dataset when expressed in the frequency-domain. This has traditionally been done with the virtual loudspeaker method [9], although recent studies have suggested to employ an alternative formulation which encodes the HRTF in the SH domain in order to operate there directly [10]. This SH-based formulation enables additional ways to preprocess the HRTF in order to improve the quality of the resulting binaural signals (e.g. see the “magnitude least squares” method, or MagLS [11]). Additionally, Ben-Hur et al. [12] have shown that the virtual loudspeaker method can be derived with the SH-based formulation (this is further discussed in Section 2), meaning that the latter provides a more general solution to the binaural decoding problem. For this reason, the SH-based formulation is employed in the present study.
Since HRTFs are typically measured or simulated offline, it is safe to assume that they can be provided with high spatial resolution. In fact, high-quality, densely sampled generic HRTFs are already publicly available [13] and there is a good amount of ongoing research on the production of individual HRTFs of similar quality (a review was provided by Guezenoc and Seguier [14]) and on the spatial upsampling of sparse HRTFs [15, 16]. Therefore, in practice, it is common to encounter situations where a binaural rendering must be obtained by pairing a low-order Ambisonics signal to a spatially dense HRTF. This mismatch can cause a loss of relevant information from the HRTF due to order truncation (as demonstrated in the Appendix), which leads to audible artefacts in the binaural signals, such as spectral colouration, loudness instability across directions and localisation blur [8, 17]. In order to mitigate these so-called truncation errors, the HRTF may be preprocessed through various methods, which are reviewed in this study, to reduce its spatial order.
It is important to note that, in addition to truncation errors, working with low-order or sparsely sampled signals can also lead to an increase in spatial aliasing and its subsequent binaural artefacts – this is the case of sound fields recorded with microphone arrays [18]. However, analysis and mitigation of aliasing errors is outside of the scope of this study, which focuses solely on truncation errors. Therefore, the contributions of this work will be most useful for applications in which Ambisonics signals can be assumed to be aliasing-free, such as deterministic plane-wave based simulations [5]. For the rendering of recorded (aliased) sound fields, the findings of this work may also be relevant, but aliasing mitigation methods should be considered – a review of these is given by Lübeck [19].
1.2 Research question and contributions
Finding the most effective HRTF preprocessing method for Ambisonics rendering, i.e. the one that best mitigates truncation errors, is an active research topic. Previous studies have compared different methods through listening tests [20–23] but the complexity and time-consuming nature of such experiments heavily limits the amount of conditions that can be tested. Ideally, one would compare all state-of-the-art HRTF preprocessing methods through a variety of metrics (e.g. localisation performance, externalisation) and for a wide range of spatial orders. However, most of the aforementioned studies only assessed one perceptual metric (usually, similarity to a reference signal) or considered just a few spatial orders in their evaluation.
Binaural models, which offer a computational simulation of binaural auditory processing and, in certain cases, allow also to predict listeners’ responses to binaural signals, are an invaluable tool that could help overcome such limitations. Using them, it is possible to rapidly perform comprehensive evaluations that would be too time-consuming to implement as actual auditory experiments, as shown by Brinkmann and Weinzierl [24]. Additionally, model-based evaluations could be extremely useful when access to human subjects is limited, such as in times of pandemic. It is likely that models will not provide accurate predictions near to the zone of perfect reproduction, but it is reasonable to expect them to provide broadly correct predictions for larger errors. This means that they could be particularly useful in the case of comparing between HRTF preprocessing methods at low spatial orders, and possibly providing insights on overall trends.
The aim of the present study is twofold: first, to propose a framework to evaluate Ambisonics-based binaural signals through auditory models; and second, to find which state-of-the-art HRTF preprocessing method performs best for a wide range of spatial orders and perceptual metrics. In particular, three different models from the Auditory Modeling Toolbox (AMT) [25] were employed in the assessment: the localisation model by Reijniers et al. [26], the externalisation model by Baumgartner and Majdak [27], and the speech reception in noise model by Jelfs et al. [28]. Furthermore, this evaluation is complemented by numerical analyses in order to relate the models’ predictions to objective metrics.
All in all, the contributions of the present study can be summarised as such:
a review of the state of the art in HRTF preprocessing methods for binaural Ambisonics rendering;
a comparison of relevant HRTF preprocessing methods’ ability to accurately render anechoic sound fields, through numerical analyses and perceptual models (localisation performance, externalisation, speech perception);
a novel method, BiMagLS, which combines two state-of-the-art methods to produce more accurate binaural signals; and
an indirect validation of the perceptual models’ ability to predict user responses to binaural signals.
This paper is structured as follows: Section 2 presents the different HRTF preprocessing methods under evaluation and introduces the novel BiMagLS; Section 3 describes the evaluation procedure, including numerical analyses and perceptual models; Section 4 presents the results; Section 5 discusses them; and Section 6 summarises the outcomes and concludes the paper. The Appendix provides some theoretical background on the Ambisonics framework and the issue of order truncation in binaural rendering.
2 HRTF preprocessing methods for Ambisonics rendering
This section presents the HRTF preprocessing methods that were compared in this study. Each method aims to obtain the SH coefficients of the HRTF (SH-HRTF) up to a limited order N which matches the order of the Ambisonics signal to be binaurally rendered, while potentially mitigating truncation errors. A discussion on the process of obtaining the SH-HRTF and the nature of truncation errors is provided in the Appendix. Implementation details are briefly described for each method and the corresponding MATLAB code is available at the BinauralSH repository in Zenodo [29].
It is worth noting that the scope of this study is limited to HRTF preprocessing methods for binaural Ambisonics rendering. Therefore, it does not cover parametric Ambisonics rendering methods, which exploit prior knowledge of the sound field [30], or methods for the mitigation of spatial aliasing artefacts (e.g. high-frequency ringing effects) [19].
2.1 Truncation (Trunc)
The baseline method to reduce the order of an SH-HRTF to N consists in simply removing all SH coefficients corresponding to order N + 1 onwards. In practice, this is often approximated by applying the discrete spherical Fourier transform (SFT) of order N to the HRTF, as defined in Eq. (A.11) in the Appendix. This method, here referred to as truncation (Trunc), does not attempt to mitigate the various truncation errors at all. Therefore, it is expected to produce large artefacts in the binaural signals, particularly for frequencies above the so-called aliasing frequency, which is proportional to the truncation order (see Eq. (A.10) in the Appendix). In other words, the Trunc method is expected to produce highly inaccurate binaural signals at low truncation orders.
2.2 Equalisation (EQ)
One of the most distinct effects of order truncation is a spectral roll-off that occurs mostly above the aliasing frequency, which leads to an undesirable direction-independent low-frequency boost in the binaural signals [31]. An easy way to mitigate this effect is to apply a global equalisation (EQ) filter to the SH-HRTF, so that its diffuse field component (i.e. its average magnitude across directions) matches the one of a reference – usually a higher-order version [31]. The EQ is direction-independent, which ensures that the perceptual cues inherent to the HRTF, such as interaural level differences (ILDs) and elevation-dependent spectral cues, will not be affected by it.
Different EQ methods have been proposed. Ben-Hur et al. [31] discuss the two most popular approaches: the first one calculates the diffuse field component of the HRTF and inverts it, resulting in HRTF-related-filters (HRF), while the second one employs “spherical head filters” (SHF) derived from an analytical spherical head model. In that study, it is shown that HRF achieves a lower spectral error than SHF does, but at the cost of being more sensitive to noise within the HRTF (e.g. inverting a notch of the diffuse field component could lead to excessive amplification and subsequent ringing artefacts), although both methods produced similar results in a listening test, by significantly improving the timbral composition of order-truncated binaural signals.
Implementation: In this study, the EQ method was implemented by first obtaining the truncated SH-HRTF as in the Trunc method (Eq. (A.11)) and then applying HRF obtained from a 44th order SH-HRTF, following ([31], Eq. (14)). Additionally, frequency-dependent regularisation [32] was employed when calculating the EQ filters to avoid excessive amplification, as implemented by Engel et al. [33, 34]. Preliminary tests showed that SHF and HRF performed similarly under these conditions, so only the latter was included in the evaluation for the sake of brevity.
2.3 Tapering (Tap)
One consequence of truncating the order of a signal in the SH domain is a “spatial leakage” effect that affects its directional pattern. This can be intuitively explained by the fact that SH coefficients are the result of a Fourier transform and, therefore, behave similarly to the well known time-frequency Fourier transform: the same way that a rectangular window applied to a time-domain signal produces undesired frequency-domain leakage in the form of side lobes along the frequency axis, “hard” order truncation in the SH domain produces side lobes in the space domain. In the case of an SH-HRTF, this effect can lead to unwanted binaural crosstalk and subsequent alterations of the ILDs, which are an essential cue for sound localisation, as shown by Hold et al. [35]. Additionally, it can cause sound sources to rapidly change loudness across directions, which is also undesirable [17].
To mitigate this spatial leakage effect, Hold et al. proposed the “tapering” method, which consists in “windowing” the SH coefficients in the same way that a time-domain signal is windowed to prevent spectral leakage. This is done by applying gradually decreasing weights to the coefficients corresponding to the higher orders. The tapering method has been shown to mitigate spatial leakage artefacts in order-truncated SH-HRTFs [35].
The tapering method is reminiscent of Max-rE weighting, a technique used to maximise sound field directivity in Ambisonics loudspeaker decoding. This method, proposed by Daniel et al. [36], applies scalar weights to the different Ambisonics channels in a way that the sound field’s energy vector (rE) from Gerzon’s sound localisation model [37] is maximised. In essence, the weights are highest for order 0 and decrease monotonically for higher spatial orders, much like the tapering window by Hold et al. Although mostly used for loudspeaker decoding, Max-rE weighting has also been employed in a binaural context by McKenzie et al. [38], where a dual-band approach is employed, applying the weighting only above the aliasing frequency.
Implementation: In this study, the tapering method (Tap) was implemented by obtaining the truncated SH-HRTF as in the Trunc method (Eq. (A.11)) and then applying Hann weights following the method by Hold et al. [35], except that a shorter Hann window was employed so that only the 3 highest orders [n ≥ (N − 3)] were tapered in order to avoid excessive attenuation, as suggested by Lübeck et al. [20]. Furthermore, a dual-band approach was employed, so weights were only applied above the aliasing frequency (Eq. (A.10)). Finally, HRF equalisation was applied to the tapered SH-HRTF as in the EQ method. Informal tests showed that dual-band tapering performed generally better than single-band (which agrees with the findings by McKenzie et al. [21]), whereas Max-rE and Hann weights performed similarly.
2.4 Time-alignment (TA)
Previous studies have shown that time-aligning all HRIRs within a dataset, essentially removing the interaural time differences (ITD), substantially reduces the effective spatial order of the resulting SH-HRTF [39]. This is illustrated in Figure 1: while a time-aligned HRTF presents a “compressed” SH spectrum that can be truncated at N = 5 and still preserve 90% of its energy at 10 kHz (Figure 1b), the non-aligned version needs up to N = 17 to preserve the same amount at that frequency (Figure 1a). This is because phase accounts for most of the spatial complexity of an HRTF; therefore, if we remove the HRIRs’ onset delays (which vary slightly across directions due to the ears not being at the origin of the coordinate system), we can considerably reduce the effective order of the SH-HRTF [16].
 |
Figure 1 SH spectra of the FABIAN HRTF [13]: (a) before preprocessing, (b) after time alignment through phase correction by ear alignment [16], and (c) after setting its phase to zero. The b90 and b99 parameters are shown, indicating the lowest spatial order that contains 90% and 99%, respectively, of the HRTF’s energy for a particular frequency bin [16]. The SH spectrum is defined as the energy of the SH-HRTF’s coefficients at every order n, according to Eq. (A.8) in the Appendix. |
When the time-alignment method (TA) is used for HRIR interpolation, ITDs can be easily reinserted in the signal without losing information. However, this cannot be done when binaurally rendering Ambisonics signals, which is why TA requires so-called bilateral Ambisonics signals, for which two receivers at the listener’s ears’ positions are used instead of a single one at the centre of the head [23]. This dual-receiver setup is straightforward to implement in an acoustic simulation, but it is worth noting that it will require separate simulations for different head rotations due to the left- and right-ear signals not sharing the same coordinate system, which contrasts with typical Ambisonics rendering in which head rotations can be easily derived ([4], Sect. 5.2.2).
Based on an evaluation with auditory models, Brinkmann and Weinzierl [24] suggested that a time-aligned SH-HRTF truncated to N = 3 could produce binaural signals that were not significantly different (in terms of localisation performance, colouration and interaural cross-correlation) from a higher-order reference, whereas a non-aligned one required N = 19. This is in agreement with a recent study by Ben-Hur et al. [23], who showed that a fourth-order binaural Ambisonics rendering generated with a time-aligned HRTF was rated by listeners as identical to a 41st-order reference in a perceptual test.
Implementation: In this study, TA was implemented with the “phase correction by ear alignment” method, as proposed by Ben-Hur et al. [16], time-aligning the HRTF before obtaining the truncated SH-HRTF with Eq. (A.11). This approach has been shown to be more robust against measurement noise than methods based on onset detection [24] and obtained promising results in recent perceptual studies [22, 23]. However, it is expected that methods based on onset detection would perform similarly [40].
2.5 Magnitude least squares (MagLS, MagLS + CC)
Following the idea of TA, Zaunschirm et al. [41] proposed a perceptually-motivated alternative method where HRIR alignment is performed only above a given frequency cutoff (fc), while ITDs are left intact below it. This frequency-dependent time-alignment (FDTA) method is based on the duplex theory [42], which establishes that ITDs (and therefore, phase) are perceptually most relevant at low frequencies, while ILDs (i.e. magnitude) are dominant at high frequencies. In parallel, the same authors presented another method called “magnitude least squares” (MagLS), which achieved superior performance than FDTA by entirely disregarding phase errors above fc [11]. Figure 1c shows how a magnitude-only version of an SH-HRTF displays an even lower effective spatial order than the time-aligned version (Figure 1b), which provides an intuition of why MagLS performs better than FDTA at low orders. In that same study, it was shown that listeners could not perceive phase errors beyond 2 kHz for continuous signals (speech) or 4 kHz if considering envelope ITD (e.g. for pulsed noise).
There exists a variant of MagLS (MagLS + CC) that employs the covariance matrix framework proposed by Vilkamo et al. [43], applying a global EQ and correcting the interaural coherence of the binaural signal, which is expected to affect important perceptual cues such as source width [41]. Zotter and Frank ([4], Sect. 4.11.3) have recommended to employ this variant for spatial orders equal or lower than 3, but this has not been thoroughly tested yet.
Note that, in contrast to TA, MagLS reduces the effective order of the SH-HRTF while preserving ITDs. Consequently, it does not require bilateral Ambisonics and is compatible with the dynamic simulation of listener’s head rotations.
Implementation: In this study, MagLS was implemented through a simple iterative procedure proposed by Zotter and Frank ([4], Sect. 4.11.2), setting the cutoff to the aliasing frequency (fc = fa) – the rationale being that, since large phase errors are expected to occur above the aliasing frequency, it is preferable to minimise magnitude errors as much as possible in that range. Furthermore, a smooth transition was applied one half-octave below and above the cutoff to avoid sharp changes in the frequency response and subsequent audible artefacts [44]. The MagLS + CC variant was implemented following ([4], Sect. 4.11.3).
2.6 Spatial subsampling/virtual loudspeakers (SpSub, SpSubMod)
The spatial subsampling method (SpSub) mitigates truncation errors by sampling an HRTF at a reduced number of directions prior to obtaining its SH coefficients [10]. This intentionally introduces spatial aliasing errors in the SH-HRTF, effectively shifting high-frequency content towards low spatial orders. Although aliasing is often undesirable, it has been shown that, in this particular case, it compensates for truncation errors to some extent [10, 17].
The SpSub method produces identical output to the popular virtual loudspeakers method, first introduced by McKeag and McGrath [9] and later employed by Noisternig et al. [45] and the developers of Google’s Resonance Audio [6], among others. The equivalence between SpSub and virtual loudspeakers is subject to choosing an appropriate sampling scheme (i.e. the number of virtual loudspeakers and their locations), as shown by Ben-Hur et al. [12]. Common sampling schemes include platonic solids (only available for N ≤ 3) [46], Gaussian quadratures [47], Lebedev quadratures [48] and T-designs [49].
McKenzie et al. [21] proposed a variant of SpSub (SpSubMod) which combines it with FDTA, dual-band Max-rE weighting (i.e. tapering) and diffuse field EQ (i.e. HRF), which was shown to perform well for orders 1 to 3.
Implementation: In this study, SpSub was implemented by obtaining a high-order (Nh = 44) SH-HRTF via discrete SFT, then sampling this SH-HRTF to an Nth order Gaussian quadrature via discrete inverse spherical Fourier transform (ISFT) (Eq. (A.12)) and finally applying the SFT again to the result, as in Eq. (A.11). Gaussian quadratures were chosen as they perform well for a wide range of truncation orders, according to Bernschütz [18] and were generated with the SOFiA toolbox [50]. Additionally, the SpSubMod variant was implemented by applying FDTA (as in [4], Sect. 4.11.1]) prior to SpSub, then applying dual-band Hann tapering and, finally, HRF equalisation [21].
2.7 BiMagLS
A novel method is introduced in this study called “bilateral MagLS”, or simply BiMagLS. This method is presented as an improved version of TA and consists of the following steps:
first, the HRTF is time-aligned as in the TA method;
for frequencies below a given threshold, the SH-HRTF of order N is obtained by means of least-squares fitting of a high-order HRTF;
for frequencies above the threshold, the SH-HRTF of order N is obtained by means least-squares fitting only the magnitude of the same high-order HRTF, while phase is estimated with the iterative procedure suggested by Zotter and Frank ([4], Sect. 4.11.2).
In other words, BiMagLS is equivalent to applying MagLS preprocessing to a time-aligned HRTF. Much like TA, this method is only compatible with bilateral Ambisonics due to the HRTF being time-aligned across the whole frequency spectrum. By combining the accurate phase reconstruction of TA and the accurate magnitude reconstruction of MagLS, this method is expected to outperform TA when rendering bilateral Ambisonics signals.
Implementation: BiMagLS is implemented by first time-aligning the HRTF using phase correction by ear alignment [16] and then generating the order-limited SH-HRTF via MagLS, as described earlier. The frequency threshold was set to 3 kHz, independently from the truncation order. This cutoff was chosen empirically, as it provided best results in informal tests. A smooth transition is applied one half-octave below and above the cutoff. For further implementation details, please refer to the conference paper by the present authors [44].
2.8 Overview
The following nine HRTF preprocessing methods were implemented: Trunc, EQ, Tap, TA, MagLS, MagLS + CC, SpSub, SpSubMod, and BiMagLS, as summarised in Table 1. The method BiMagLS, which combines the qualities of TA and MagLS and is presented as a direct improvement of the former, has been introduced in this work. Of the nine methods, two of them (TA and BiMagLS) assume a time-aligned HRTF and cannot be used directly to binaurally render a standard Ambisonics signal. Even though they are not directly comparable to the other methods, they have been included for the sake of completeness, as they are still valuable for HRTF interpolation and for rendering bilateral Ambisonics signals, i.e. measured at the ears’ positions.
Evaluated HRTF preprocessing methods.
A previous perceptual study by Lübeck et al. [20] has already compared Trunc, EQ, Tap, SpSub and MagLS for the binaural rendering of microphone array recordings, using a dummy-head recording as the reference. Their data showed that all methods achieved an increase in quality compared to a low-quality anchor (low-passed diotic signal), but no significant differences were observed among the methods at high orders. One limitation of said study was that only three spatial orders were evaluated (3, 5 and 7) and only one perceptual metric (similarity to the reference) was evaluated. In the present study, we aim to complement their results by assessing some additional methods, a wider range of spatial orders and several perceptual metrics. This is achieved thanks to a model-based evaluation and complementary numerical analyses, which are detailed in the next section.
3 Evaluation methods
The previous section introduced the nine HRTF preprocessing methods to be assessed. For the evaluation, a publicly available HRTF (FABIAN dummy head with an upright head-torso orientation [13]) was employed. The HRTF was measured for 11 950 directions and HRIRs had a length of 2048 samples (zero-padded from 256), sampled at a rate of 44.1 kHz. Informal tests also evaluated a numerically simulated HRTF of the FABIAN dummy head and the Neumann KU100 HRTF measured by Bernschütz [51], but the results were similar to the current ones and ultimately not reported here for the sake of brevity.
SH-HRTFs of orders 1 to 44 were generated with every preprocessing method as indicated in Section 2. Then, from each order-limited SH-HRTF, HRIRs were interpolated to the original 11 950 directions via ISFT (Eq. (A.12)). In order to evaluate the methods that operate with fully time-aligned HRTFs (TA and BiMagLS), the phase correction was reversed after interpolation by undoing the ear alignment process. However, it should be noted that said phase correction reversal is generally only possible when performing HRTF interpolation and not when rendering standard Ambisonics signals. Therefore, the results for TA and BiMagLS should be interpreted only in the context of HRTF interpolation and rendering of bilateral Ambisonics signals.
Some subsets of directions were given special attention: those in the horizontal plane (180 directions), those in the median plane (also 180) and those closest to a 110-point Lebedev grid. The latter was chosen for being evenly sampled around the sphere and easily reproducible, and because 110 points were found to be enough to provide relevant insights, but not too many to substantially slow down the execution of the perceptual models.
Finally, the differences between the interpolated and the original HRIRs were assessed in an initial analysis (magnitude and phase errors, interaural cues, direction-dependency) and through auditory models, as detailed in the following subsections.
It is worth noting that interpolating an HRIR for a given direction is equivalent to rendering a single anechoic far-field source, i.e. a plane wave. Therefore, the preprocessing methods are here evaluated for the scenario of binaurally rendering such a sound source. The methods’ ability to deal with reverberant or diffuse sound fields is not explicitly assessed, the implications of which are discussed in Section 5.
3.1 Initial analysis
The first step was to obtain magnitude and phase interpolation errors for the 110 positions closest to the Lebedev grid. Magnitude error was calculated as the absolute difference between the log-magnitude of the original HRIRs and the interpolated ones, averaged across directions. Phase error was calculated as the absolute difference between the interaural phase delay of the original HRIRs and the interpolated ones, averaged across directions. Interaural phase delay was obtained by subtracting phase delay (unwrapped phase, calculated with the unwrap function from MATLAB R2020b, divided by frequency) of the right channel from the left one in an HRIR pair. We expected that the analysis of interpolation errors would offer a first insight on the accuracy of a given HRTF preprocessing method. For instance, large magnitude errors are expected to distort monoaural cues and, by extension, externalisation [27] and vertical localisation performance [52], as well as ILDs. On the other hand, large phase errors are expected to affect ITDs and low-frequency lateral localisation, being most perceptually relevant below 2 kHz (perhaps 4 kHz, for some stimuli), according to Schӧrkhuber et al. [11].
The second step was to estimate the interaural cues, namely ITDs and ILDs, for the 180 horizontal-plane directions on both the original and interpolated HRTFs. This would complement the interpolation error data and allowed for a more perceptually-motivated analysis. ITD was estimated with the MaxIACCe method, after applying a low-pass filter (3 kHz) to the HRIRs, as described by Katz and Noisternig [53]. ILD was estimated according to McKenzie et al. [54], by calculating it separately for 30 equivalent rectangular bandwidths (ERB) on a high-passed (1.5 kHz) HRIR and then averaging those. Interaural coherence was also initially considered, but preliminary tests showed that it was generally very close to the maximum value (1) in most cases, so it did not provide relevant insights for the present study. This was expected, given that the current evaluation is of anechoic sources, whereas interaural coherence has been found to be mostly related to externalisation of reverberant binaural signals [55]. Future studies including reverberant conditions should include the evaluation of interaural coherence.
The third step was to analyse how the magnitude interpolation errors varied across different directions. This was expected to provide insights on the spatial leakage effects described in Section 2.3. Instead of looking at the direction-dependent errors for each frequency bin separately, we opted for “collapsing” the frequency axis by using the model by Armstrong et al. [56]. This model translates magnitude deviations into estimated loudness differences, and performs a weighted average over the full frequency range by means of equivalent rectangular bandwidths (ERBs) [57]. As a result, we estimate the magnitude of the HRTF for a given direction as a single scalar measured in sones. The loudness difference between a given interpolated HRTF and a reference is referred to as the perceptual spectral difference (PSD), which quantifies the distance between two HRTFs’ magnitude spectra in a perceptually-motivated way, as shown by McKenzie et al. ([54], Sect. 4.1).
3.2 Auditory models
Finally, the interpolated HRIRs were evaluated through binaural models. First, localisation performance was estimated using the ideal-observer model by Reijniers et al. [26], as implemented by Barumerli et al. [58] in the AMT. The model predicted localisation performance 100 times for each of the 110 Lebedev grid directions, in order to account for the stochastic processes implemented by the model, which aim to replicate the listener’s uncertainty when performing a localisation task. Then, the overall lateral and polar accuracy and precision were calculated. This model estimates sound localisation performance on the whole sphere, unlike previous models like the ones by May et al. [59] (lateral localisation only) or Baumgartner et al. [52] (sagittal localisation only), which allows for more insightful predictions. A key feature is its Bayesian modelling approach, which allows to predict listener’s uncertainty when assessing the location of a sound source. This was crucial for the purpose of this study, considering that one of the effects of spatial order truncation is localisation blur, or sound sources appearing wider than they should [8]. It was expected that a wide sound source and a narrow one would, on average, be both localised at the correct position (same accuracy), but the narrow source would yield lower localisation variance than the wide one (different precision). Therefore, the localisation precision predicted by the model was expected to be valuable in this evaluation. For an example of analysis of localisation accuracy and precision, the reader is referred to Majdak et al. [60].
Second, externalisation was predicted for the 180 median-plane directions, using the model by Baumgartner and Majdak [27], as implemented in the AMT, and then averaged across said directions to obtain a single value. This model predicts externalisation as a weighted sum of two parameters: monoaural spectral similarity and interaural broadband time-intensity coherence. It is worth noting that the model considers a static (non-head-tracked) and unimodal (auditory information only) binaural rendering. Externalisation can be influenced by several factors that have not yet been accounted for in existing binaural models, such as early reflections and reverberation, visual information, listener expectations (see the “divergence effect” [61]) and dynamic cues (especially when caused by self-movements) [62]. However, these additional factors are not necessarily influenced by the independent variables used in this study (spatial order, HRTF preprocessing method) and, therefore, a static externalisation estimation was considered a valuable metric for our purposes.
Finally, speech reception in noise was evaluated with the model by Jelfs et al. [28], as implemented in the AMT. The model predicted spatial release from masking (SRM), expressed as the benefit in dB provided by the better-ear and binaural unmasking effects, for one target source and one masker (multiple maskers could have been used as well, but this was not considered beneficial for the purpose of the current study). It was run 180 times per HRTF, changing the masker position between each of the horizontal plane directions, while the target was always placed in front of the listener. No reverberation was included and the masker was set to the same level as the target source. Even though the model is intended to assess reverberant signals, it could provide useful insights on perceived source separation in a practical application of anechoic binaural rendering (e.g. a videoconference with spatial audio).
4 Results
4.1 Initial analysis
Figure 2 shows how magnitude and phase interpolation errors varied with spatial order within the Trunc condition, which was chosen as a baseline for not implementing any mitigation of truncation-related artefacts (see Section 2). It can be seen how errors rapidly increase after the aliasing frequency is surpassed, which depends on the order, e.g. 0.6 kHz for N = 1, 3 kHz for N = 5, etc. Clearly, lower spatial orders lead to lower aliasing frequencies and larger overall errors, as expected. For the highest tested order (44), with an aliasing frequency well above the audible range, the average magnitude error is generally below 1 dB and the phase delay error is mostly under 20 μs, suggesting that this SH-HRTF will not produce audible artefacts.
 |
Figure 2 Absolute HRTF magnitude errors (left ear) and interaural phase delay errors, averaged across 110 directions in an approximate Lebedev grid. HRTFs were interpolated from truncated SH-HRTFs (Trunc method) for five different spatial orders (1, 10, 20, 30, 44). The dotted lines indicate an approximation of the just noticeable differences: 1 dB for magnitude and 20 μs for phase delay. |
The same interpolated HRTFs are compared in terms of ITD and ILD on the horizontal plane in Figure 3. A one-way analysis of variance (ANOVA) detected a significant effect of spatial order on the ITD error [F(5, 1074) = 389.5992, p < 0.001]. A Tukey post-hoc revealed significant differences among the data groups as indicated with dashed lines in the figure, considering a significance level of 0.05. Regarding ILD errors, an ANOVA also detected a significant effect of spatial order [F(5, 1074) = 309.8585, p < 0.001], with the Tukey post-hoc test revealing significant differences as indicated in the figure.
 |
Figure 3 Top: Interaural time differences (ITD) and interaural level differences (ILD), plotted as a function of azimuth on the horizontal plane for the same HRTFs evaluated in Figure 2. Bottom: violin plots showing the absolute ITD and ILD errors for each HRTF on the horizontal plane, where the horizontal dotted lines represent the approximate JNDs in anechoic conditions, according to Klockgether and van de Par [63], and the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
The fact that the interaural differences for N = 1 differed significantly from the rest could be anticipated from the large magnitude and phase errors reported earlier. On the other extreme, the 44th-order interpolated HRTF obtained very similar results to the reference, which is in agreement with its low interpolation errors. The data also shows that ITD converged towards the reference at an earlier order (between 5 and 10) than ILD (between 30 and 44). This can be explained by the fact that the ITD estimation method mainly considers frequencies below 3 kHz, whereas the ILD estimation method is mostly influenced by frequencies above 1 kHz (see Section 3) and, therefore, is affected more by high-frequency truncation errors.
The nine HRTF preprocessing methods are compared in Figure 4 for a spatial order of N = 3. It can be seen how magnitude and phase errors increase considerably above the aliasing frequency (marked with a vertical dashed line), as expected. The largest magnitude error was obtained for Trunc and the smallest ones, for MagLS and BiMagLS, which is in agreement with the instrumental evaluation in [20]. The EQ method displayed smaller magnitude errors than Trunc, which showcases the benefits of the diffuse field equalisation filter. In terms of phase, all methods displayed similarly small errors below the aliasing frequency. Above that threshold, TA and BiMagLS both obtained the smallest errors overall, which was expected since these methods are able to accurately reconstruct ITDs, assuming a correct implementation of bilateral Ambisonics. Among the methods that do not fully time-align the HRTF, relatively large phase errors (one order of magnitude higher than the estimated JND) were observed above the aliasing frequency for all methods, with SpSub obtaining slightly smaller errors than the rest.
 |
Figure 4 (a) Absolute HRTF magnitude (left ear) and (b) interaural phase delay errors, averaged across 110 directions in an approximate Lebedev grid. HRTFs were preprocessed with the nine methods at N = 3 and interpolated. The horizontal dotted lines indicate an approximation of the just noticeable differences: 1 dB for magnitude and 20 μs for phase delay. The vertical dashed line indicates the aliasing frequency. |
Data of ITD and ILD errors for the different preprocessing methods and a spatial order of N = 3 are reported in Figure 5. ANOVAs identified a significant effect of the method on ITD error [F(8, 1611) = 113.0652, p < 0.001] and ILD error [F(8, 1611) = 100.0632, p < 0.001]. Post-hoc Tukey tests detected significant differences (p < 0.05) among the methods as reported at the bottom of Figure 5.
 |
Figure 5 Top: Interaural time differences (ITD) and interaural level differences (ILD), plotted as a function of azimuth on the horizontal plane for HRTFs preprocessed with the nine methods at N = 3 and interpolated. Bottom: violin plots showing the absolute ITD and ILD errors for each HRTF on the horizontal plane, where the dotted lines represent the approximate JNDs in anechoic conditions, according to Klockgether and van de Par [63], and the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
The data showed how TA and BiMagLS are, as expected, the methods with most accurate ITDs by a large margin (for N = 3 and, again, assuming a correct bilateral Ambisonics implementation), while other methods performed poorly in comparison, as a consequence of large phase errors, with SpSub performing slightly better than the rest. In terms of ILD, the trend seems to agree with the magnitude errors discussed earlier, with the largest deviations being produced by Trunc, EQ and SpSub, which displayed lower ILDs at lateral directions. These low lateral ILDs are attributed to the binaural crosstalk caused by the spatial leakage effect discussed in Section 2.3. The methods with the lowest ILD error are generally the same ones that displayed the smallest magnitude errors: BiMagLS, MagLS, MagLS + CC, SpSubMod and TA. Detailed data on interaural errors is reported in [64].
The interpolated (N = 3) left-ear HRTFs’ magnitude per direction is illustrated in Figure 6 by means of their estimated loudness. These plots can be useful to identify spatial leakage effects, e.g. by looking at the ripples in the Trunc, EQ and, to a lesser extent, SpSub plots. For instance, the EQ plot displays a clearly higher loudness than the reference plot at the contralateral positions (around −90° azimuth, 0° elevation), which is a consequence of the binaural crosstalk effect described in Section 2.3. These artefacts are likely related to the high ILD errors observed earlier and may also lead to undesirable loudness instability in the binaural signals, i.e. sound sources substantially varying their loudness depending on their position [17]. In contrast, the Tap plot does not display such artefacts when compared to Trunc or EQ, suggesting that the preprocessing method has succeeded in mitigating spatial leakage, as intended. The rest of the methods (MagLS, MagLS + CC, TA, SpSubMod, BiMagLS) do not display evident spatial leakage effects.
 |
Figure 6 Top: Estimated loudness, which was chosen as a perceptually-motivated representation of the magnitude, of the left-ear HRTF. The top-left plot shows the Reference (original HRTF) and the other plots show HRTFs preprocessed with the nine methods at N = 3 and interpolated over all available directions (11 950). Bottom: violin plots showing the PSD between each method and the reference for the approximate 110-point Lebedev grid (lower is better), where the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
The bottom plot of Figure 6 displays the PSD between each interpolated HRTF and the reference one, sampled at the approximate 110-point Lebedev grid. An ANOVA revealed a significant effect of the method on the PSD [F(8, 981) = 184.2456, p < 0.001] and a Tukey post-hoc test identified significant differences among the methods (p < 0.05) as indicated in the figure.
We observe that the methods that achieved the lowest (best) PSD when compared to the reference were MagLS and BiMagLS (average of 0.27 sones), closely followed by MagLS + CC, TA and SpSubMod, all below 0.5 sones on average. The methods SpSub, EQ and Tap show a higher average PSD in comparison, up to 0.87 sones. Finally, the highest average PSD was obtained for Trunc, with a median error of 1.16 sones. This trend is the same one that was observed when analysing the magnitude errors, which was expected, given that PSD is essentially a frequency-averaged representation of magnitude error.
The PSD of each method, averaged over the 110 points, is shown as a function of spatial order at the top left plot of Figure 7. Here, the 110 points were considered as a population rather than a sample and, therefore, inferential analysis was not conducted. The overall trend seems to be that PSD decreases monotonically with spatial order, as expected. According to this metric, the best performer was BiMagLS, followed by MagLS, MagLS + CC, TA and SpSubMod, while the worst one was Trunc. Differences among methods were found to be relatively large for lower orders and become smaller for higher orders, falling below 0.03 sones for any pair of methods above N = 30. For N ≤ 6, MagLS and BiMagLS obtained the best results, especially if compared with the methods SpSub, EQ and Tap. For N > 6, BiMagLS still obtained the best results, while TA performed sligthly better than MagLS. It is worth noting that SpSubMod performed overall better than SpSub and also that MagLS + CC did not outperform MagLS, according to this metric, even for the lowest spatial orders.
 |
Figure 7 Binaural models’ output for HRTFs that were preprocessed with different methods and interpolated for spatial orders 1 to 44. Top left: left-ear perceptual spectral difference (PSD [56]) with the reference, averaged across the approximate 110-point Lebedev grid (lower is better). Top middle and top right: lateral and polar localisation precision, as estimated by the model of Reijniers et al. [26] for the same 110 directions (lower is better). Bottom left: externalisation, as estimated by the model of Baumgartner and Majdak [27] for 180 median plane directions (higher is better). Bottom right: spatial release from masking (SRM) in dB, as estimated by the model of Jelfs et al. [28], averaged for 180 masker positions in the horizontal plane. Reference data (black dotted line) was obtained from the original HRTF. Detailed data in tabular form is provided in [64]. |
Overall, TA and BiMagLS showed the most promising results according to the initial analysis, considering their accurate ITD reconstruction and small magnitude errors, particularly in the case of the latter. However, as mentioned earlier, these results are subject to the assumption that bilateral Ambisonics signals are accurately generated. Among the rest of methods, all of which are compatible with standard Ambisonics signals, MagLS displayed the smallest magnitude and ILD errors for N = 3, as well as the lowest PSD with the reference for most truncation orders. However, other methods such as SpSub obtained smaller ITD errors than MagLS at N = 3. Further evaluations are needed to explore which method performs best at various spatial orders. This is discussed in the next subsection.
4.2 Auditory models
Figure 7 shows the auditory models’ output as a function of spatial order for the nine preprocessing methods. For all data, the general trend seems to be that all methods converge towards the reference as spatial order increases, as suggested by the initial analysis.
Lateral precision, defined as the circular standard deviation of localisation estimates in the lateral dimension [60], is shown at the top middle plot of Figure 7. Compared to the other metrics, it seems to converge quite early, with all methods displaying an error below 2° for N = 20. This is likely due to the strong influence of ITDs in lateral localisation and the fact that ITDs converge at a relatively early order (see Figure 3) due to not being much affected by high-frequency truncation errors. BiMagLS and TA showed the best performance overall, probably because of their small phase errors, assuming accurate bilateral Ambisonics reproduction, as dicussed in the previous section. Other methods performed poorly for N < 5, likely due to inaccurate ITDs, e.g. as reported in the initial analysis. For N ≥ 5, when ITDs become more accurate, all methods perform similarly well except Trunc, EQ and SpSub; this is attributed to their higher ILD errors, reported in Figure 5.
Polar precision, defined as the circular standard deviation of localisation estimates in the polar dimension [60], is shown at the top right plot of Figure 7. In this case, errors were relatively large for all methods at low orders and converged between orders 20 and 25. BiMagLS and TA displayed the best performance in general, followed by SpSubMod, MagLS and MagLS + CC, while the rest showed larger errors in comparison.
Note that lateral and polar accuracy (i.e. mean localisation error) were also assessed but no important differences among methods or spatial orders were found, so they were not reported for the sake of brevity.
Externalisation (bottom left in Figure 7), computed as a scalar between 0 and 1, seemed to follow a very similar trend to PSD, with the methods MagLS, BiMagLS and MagLS + CC obtaining the best performance overall, with values above 0.9 for orders as low as 3. Like with PSD, the methods Trunc, EQ, Tap and SpSub displayed comparatively worse performance than the rest. This similarity in trends between externalisation and PSD is attributed to the fact that the externalisation model assigns a considerable weight to monoaural spectral similarity, which is highly related to the PSD metric [27].
Finally, spatial release from masking (SRM, bottom right in Figure 7) also seemed to display a strong dependence on spatial order, but all methods quickly converged towards the reference as the order increased. The methods BiMagLS and TA showed good performance at low orders, being generally within 1 dB from the reference, followed closely by MagLS and SpSubMod. On the other hand, Trunc, EQ and SpSub displayed comparatively worse performance up to N = 15 where all methods converge within 0.1 dB from the reference.
5 Discussion
5.1 Comparing HRTF preprocessing methods
The binaural models’ output mostly agreed with the initial analysis. For instance, magnitude interpolation errors were shown to correlate with the disruption of monaural spectral cues, loudness stability and ILDs, which translated to lower localisation precision, externalisation and speech intelligibility in the presence of maskers. As a consequence, methods that achieved smaller magnitude errors, such as MagLS, BiMagLS or TA, displayed better results according to those metrics. The same can be said about phase errors correlating to lateral precision, given that TA and BiMagLS outperformed other methods in this aspect. Similarly, increasing spatial order led to better performance, regardless of the preprocessing method.
Among methods that do not assume a time-aligned HRTF and, thus, are compatible with standard Ambisonics signals, MagLS displayed the best performance in terms of PSD and externalisation. MagLS + CC did not display clearly superior results to MagLS overall, indicating that the additional feature of the covariance constraint may not provide an obvious benefit. However, future evaluations with reverberant sound fields may lead to different results, as MagLS + CC is expected to restore interaural coherence more accurately than other methods, which is an important feature for accurately rendering reverberant binaural signals [55]. For lateral and polar precision, the best results were often disputed between MagLS, MagLS + CC and SpSubMod, depending on the spatial order, with no method being clearly superior overall. For SRM, most methods performed well since relatively low orders, with the best performance again being shared between MagLS and SpSubMod.
Overall, the data suggests that the choice of preprocessing method might have a rather small impact on the perceived quality for spatial orders beyond 20 (perhaps smaller) but it can definitely be impactful for the lowest orders. Among the tested methods, MagLS performed well across the board and can be recommended as a good option to preprocess HRTFs for binaural rendering of Ambisonics signals of any spatial order. For orders below 5, MagLS displayed higher ITD errors than other methods such as SpSub, but these do not seem to have negatively impacted lateral localisation precision, according to the models. Regardless, this recommendation should be validated by listening tests, e.g. comparing MagLS and SpSub in a lateral sound localisation task.
On the other hand, two of the methods (TA and BiMagLS) assumed a different rendering scenario in which the Ambisonics signal is measured bilaterally at the ears’ positions, which is why they are discussed separately here. For these methods, the validity of the results is subject to the bilateral signal being properly obtained, so that phase is reconstructed accurately. Under this assumption, these two methods outperform most of the alternatives across most spatial orders, with BiMagLS being the best performing method overall for the tested metrics. This would confirm the hypothesis that BiMagLS is a direct upgrade over TA, on which it is based, due to its more accurate magnitude reconstruction (leading to better results for all metrics and spatial orders, as shown in Figure 7) without compromising ITDs. However, a perceptual comparison of TA and BiMagLS should be performed to formally confirm that the predicted differences between the two methods are perceptually relevant.
5.2 Validity of the model-based assessment and limitations
The models’ predictions were generally in line with results from previous perceptual experiments, namely:
EQ and SpSub were more similar to a reference than Trunc in terms of timbre (i.e. PSD) but not so much in terms of localisation performance for orders 3 and 6, as reported by Sheaffer and Rafaely [65];
SpSubMod was more similar to a reference than SpSub for orders 1 to 3, as reported by McKenzie et al. [21];
SpSub showed higher loudness stability than Trunc for orders 2, 4 and 10, as reported by Ben-Hur et al. [17];
MagLS was more similar to a reference than SpSub for orders 1 to 5, as reported by Lee et al. [66];
TA achieved better lateral localisation performance than MagLS for orders below 5 while being similar across other metrics, which could result in an overall more accurate rendering, as reported by Ben-Hur et al. [23] (note that Ben-Hur et al. reported relatively low MagLS ratings, which may have been caused by artefacts around the cutoff frequency, whereas these were avoided in the present study by smoothing the frequency response);
TA at order 2 was more similar to a reference than Tap at order 6, as reported by Ben-Hur et al. [22]; and
MagLS, SpSub, Tap, EQ were all more similar to the reference than Trunc for orders 3, 5 and 7, as reported by Lübeck et al. [20].
These similarities support the argument that binaural models could be a valuable tool for evaluations as the present one, and might be a valid alternative to real listening experiments. However, it is important to also point out the limitations of this model-based assessment. First of all, the models may not always be perfectly calibrated. For instance, the localisation model may have over- or underestimated the listener’s uncertainty, resulting in a a biased estimation of localisation precision [58]. However, even if models show some bias compared to the real world, they could still be useful for relative comparisons such as the one performed here, particularly to detect overall trends within a large set of test conditions, being much faster to run than a listening experiment.
Perhaps a more important limitation of this evaluation was the lack of dynamic listening conditions (allowing movements of sources or listener), which are possible in real listening experiments, but are not supported by current binaural models, to the extent of the authors’ knowledge. Dynamic conditions could potentially affect the perception of externalisation [62] and of the “smoothness” of the sound field [67]. We can get some insights by looking at Figure 6, which suggests that MagLS will provide a smoother rendering than Trunc, for instance. However, proper evaluation of dynamic conditions are left for future work, when appropriate auditory models become available.
Finally, another limitation of this study was the lack of evaluation of reverberant sound fields. Initially, it was considered to run the experiment under different reverberation conditions, e.g. anechoic, small room, large room. However, the inclusion of this variable was finally left for a follow-up study for two reasons. First, to prevent the study to become too complex as it already included many test conditions (9 methods, 44 spatial orders, 3 perceptual models). And second, because it is assumed that the anechoic condition is the most critical scenario for binaural Ambisonics rendering, given that previous studies have shown that diffuse reverberation is less affected by truncation artefacts than the direct sound [67, 68], and therefore may act as a masker (this was confirmed by informal listening tests).
5.3 Future work
Future studies, similar to the present one, could employ a higher number of HRTFs in order to assess how the models’ prediction is affected by the choice of HRTF. Also, follow-up experiments should be conducted including reverberant conditions, in which it would be interesting to study additional binaural metrics such as interaural coherence, which has been linked to externalisation in reverberant scenarios [55]. It is speculated that, in such a scenario, MagLS + CC could outperform other methods like MagLS due to its more accurate reconstruction of interaural coherence.
More importantly, the natural next step would be to validate the models’ outputs through an actual listening experiment, assessing the same perceptual metrics that were modelled in this work. Since auditory models do not typically account for cognitive processes (which can influence localisation and other metrics), a perceptual evaluation should provide more meaningful data. For such future evaluation it might not be necessary to include all test conditions such as the 44 spatial orders. Instead, it would be more efficient to employ an adaptive procedure (perhaps informed by artificial intelligence) with the current results as a starting point, e.g. to find the minimum spatial order at which some perceptual effect becomes apparent. This could open up an interesting avenue in auditory perception research, where not only experimental data is used to inform models, but also the other way around.
Finally, a formal perceptual evaluation of the novel BiMagLS method is left for a future study, as this falls outside the scope of the present paper.
6 Conclusions
The present study assessed the performance of a selection of state-of-the-art HRTF preprocessing methods for the binaural rendering of order-limited Ambisonics signals. This was done with the help of auditory models, which allowed to conduct an evaluation that would have been highly time-consuming to implement through actual listening tests.
Results suggested that, from the reviewed methods, MagLS displayed the best results across the evaluated metrics and most of the tested spatial orders, and is therefore the recommended method for the binaural rendering of order-limited Ambisonics signals. However, this recommendation is subject to change, as further evaluations considering sound fields with reverberation or spatial aliasing errors should be carried out.
Additionally, the novel BiMagLS method was proposed as an improved version of the time-alignment method (TA), which was supported by the outcomes of the evaluation. Therefore, the BiMagLS method is recommended for the rendering of bilateral Ambisonics signals and, in general, for low-order spherical harmonics HRTF interpolation.
The models’ predictions were shown to be consistent with previous perceptual data. This makes a strong point in favour of model-based evaluations in auditory perception research, considering that they require a fraction of the time and effort of actual listening experiments, while providing reproducible results.
Conflict of interest
Authors declared no conflict of interests.
Data Availability Statement
Implementations of the models [26–28] and the simulations (exp_engel2021) used in this article are publicly available as part of the Auditory Modeling Toolbox (AMT, https://www.amtoolbox.org) [25] in the release of the version 1.1.0 available as a full package for download [69]. Also, the methods discussed in this paper are available online through the BinauralSH repository in Zenodo: https://doi.org/10.5281/zenodo.4633933 [29].
Appendix
Ambisonics framework and order truncation
The goal of this appendix is to provide some mathematical foundations about the Ambisonics framework. This will give context on the issue of spatial order truncation which the HRTF preprocessing methods try to mitigate. Most of the notation is borrowed from Rafaely and Avni [70], Zotter and Frank [4] and Bernschütz [18].
A.1 Spherical Fourier transform
The Ambisonics framework allows for expressing spatial audio signals (e.g. a three-dimensional sound field or an HRTF) as spherical functions described by SH coefficients, which enables various useful post-processing and playback options. The process of obtaining the SH coefficients from a spatial audio signal is known as the spherical Fourier transform (SFT). Similarly to how the Fourier transform is used to express a time-domain signal as a series of frequency coefficients, the SFT can express a signal sampled at discrete directions over a sphere as a series of SH coefficients ([7], Chap. 1.4). Given a function x(θ, ϕ) sampled at a set of points, where θ is the elevation measured downwards from the north pole and ϕ is the azimuth measured counterclockwise from the front, and the radius is fixed, its SH coefficients are calculated with the SFT, as defined by Rafaely and Avni ([70], Eq. (1)):
where  are the normalised, real-valued spherical harmonics of order n and degree m, as defined by Zotter and Frank ([4], Eq. (A.35)):
are the normalised, real-valued spherical harmonics of order n and degree m, as defined by Zotter and Frank ([4], Eq. (A.35)):
with
and where  is the associated Legendre function, calculated as described by Williams ([71], Eq. (6.29)). Applying the SFT to a signal is sometimes called “Ambisonics encoding”. Analogously, the inverse spherical Fourier transform (ISFT) or “Ambisonics decoding” is defined as:
is the associated Legendre function, calculated as described by Williams ([71], Eq. (6.29)). Applying the SFT to a signal is sometimes called “Ambisonics encoding”. Analogously, the inverse spherical Fourier transform (ISFT) or “Ambisonics decoding” is defined as:
Note that SH conventions vary depending on the scientific field and the author’s style. In this work, we chose the real-valued formulation of Zotter and Frank’s [4], which is commonly used in Ambisonics and is more convenient than complex-valued ones because it does not involve the complex conjugation of the  term in Eq. (A.1), and is therefore simpler to implement while providing the same results. The reader is referred to the work by Poletti [72] and Andersson [73] for further discussion on SH conventions and their use in Ambisonics.
term in Eq. (A.1), and is therefore simpler to implement while providing the same results. The reader is referred to the work by Poletti [72] and Andersson [73] for further discussion on SH conventions and their use in Ambisonics.
A.2 Binaural rendering of a sound field
We define a sound field as a sum of an infinite number of plane waves (PW) and we describe it with a PW density function, a(f, θ, ϕ), which varies over frequency and direction. For its binaural rendering, the sound pressure at the left ear can be calculated in the frequency domain by multiplying each PW with the corresponding left-ear HRTF hl(f, θ, ϕ) across all directions, as described by Rafaely and Avni ([70], Eq. (7)):
By substituting a(f, θ, ϕ) and hl(f, θ, ϕ) with their SH representation (Eq. (A.4)) and applying the SH orthogonality property described by Rafaely ([7], Eq. (1.23)), we obtain:
where anm(f) and  are the SH coefficients of a(f, θ, ϕ) and hl(f, θ, ϕ), respectively, as defined by Rafaely and Avni ([70], Eqs. (8)–(10)). We may also refer to anm(f) as the Ambisonics signal and to
are the SH coefficients of a(f, θ, ϕ) and hl(f, θ, ϕ), respectively, as defined by Rafaely and Avni ([70], Eqs. (8)–(10)). We may also refer to anm(f) as the Ambisonics signal and to  as the SH-HRTF. Note that this same process can be performed for the right-ear HRTF hr(f) to obtain the pressure at the right ear, pr(f), to produce the complete binaural signal. Hereafter, the left and right superscripts are omitted for brevity, and it is assumed that both ears are processed separately.
as the SH-HRTF. Note that this same process can be performed for the right-ear HRTF hr(f) to obtain the pressure at the right ear, pr(f), to produce the complete binaural signal. Hereafter, the left and right superscripts are omitted for brevity, and it is assumed that both ears are processed separately.
A.3 Order truncation and aliasing frequency
In practice, the infinite summation in Eq. (A.6) must be truncated at some finite order N, which yields an approximation of the true binaural signal:
where the superscripts indicate that the SH coefficients have been truncated at order N. This order truncation causes a loss of information that can lead to audible artefacts in the binaural signal  , such as over-emphasised low frequencies or poor localisation of sound sources [8]. The cause of these artefacts can be intuitively explained by looking at the HRTF’s SH spectrum, defined as the energy of its SH coefficients for each order (n) [16]:
, such as over-emphasised low frequencies or poor localisation of sound sources [8]. The cause of these artefacts can be intuitively explained by looking at the HRTF’s SH spectrum, defined as the energy of its SH coefficients for each order (n) [16]:
Looking at the SH spectrum in Figure 1a, we observe that an HRTF’s high-frequency content is mainly “stored” at high orders, meaning that order truncation will cause a loss of mostly high-frequency content, which explains the spectral colouration described by Avni et al. [8]. The dotted lines, which roughly indicate the upper boundary of the SH spectrum, increase almost linearly with frequency. In fact, previous work has shown that the minimum truncation order (Na) required to contain an HRTF’s SH spectrum up to a given frequency fa can be approximated by:
where c is the speed of sound and r is the radius of the smallest sphere surrounding the listener’s head [16]. Conversely, it can also be said that, for a given truncation order, there exists an approximate “spatial aliasing frequency” (fa) up until which an HRTF’s SH spectrum can be represented without incurring into major artefacts, as described by Bernschütz ([18], Sect. 3.8):
Therefore, assuming a speed of sound of c ≃ 343 m/s and a nominal head radius of r ≃ 0.0875 m [16], a truncation order of at least 32, if not higher, would be needed to represent an HRTF in the SH domain to a reasonable degree of accuracy within the audible spectrum (up to 20 kHz), which agrees with Figure 1a.
However, the truncation order is sometimes imposed in practice as a constraint of the binaural rendering application, usually because the Ambisonics signal is given with a limited order, as discussed in Section 1. Since the order of a binaural rendering is dictated by the lowest order between anm(f) and hnm(f) [12], the Ambisonics signal will impose its lower order even if the SH-HRTF has a higher one – the opposite could also happen, but it is less common. Therefore, the SH-HRTF’s order must be reduced.
A.4 Reducing the SH-HRTF’s order
The most straightforward way to reduce an SH-HRTF’s spatial order to N, so it matches the Ambisonics signal, is to simply truncate it by removing all SH coefficients from N + 1 onwards. In practice, this is typically approximated by solving the discrete version of the SFT in a least-square sense, as derived by Ben-Hur et al. [16]. This can be expressed in matrix notation as:
where  is a matrix representation of the truncated SH-HRTF [
is a matrix representation of the truncated SH-HRTF [ ] with as many rows as frequency coefficients and as many columns as SH coefficients; h is a matrix representation of the HRTF [h(f, θ, ϕ)] with as many columns as measured directions; YN is a matrix containing the spherical harmonics up to order N sampled at the HRTF’s directions; and † denotes the pseudoinverse. Note that there is also a discrete version of the ISFT, which is typically employed to interpolate an HRTF (
] with as many rows as frequency coefficients and as many columns as SH coefficients; h is a matrix representation of the HRTF [h(f, θ, ϕ)] with as many columns as measured directions; YN is a matrix containing the spherical harmonics up to order N sampled at the HRTF’s directions; and † denotes the pseudoinverse. Note that there is also a discrete version of the ISFT, which is typically employed to interpolate an HRTF ( ) for a desired set of directions [16]:
) for a desired set of directions [16]:
Truncating and interpolating an HRTF without preprocessing (essentially, the Trunc method from Section 2) leads to the audible artefacts discussed earlier. Several approaches have been proposed to reduce the order of an SH-HRTF in such a way that such artefacts are alleviated and binaural renderings are more accurate – these are the other methods reviewed in Section 2.
Note that the “coarse” sampling of the sound field or the HRTF can also lead to spatial aliasing errors, especially when dealing with low-order microphone array recordings [18]. However, this work assumes that both anm(f) and hnm(f) are alias-free (e.g. as in a plane-wave-based audio engine that has access to a high-order HRTF [5]) and focuses on truncation-related errors.
References
- F.L. Wightman, D.J. Kistler: Headphone simulation of free-field listening. I: Stimulus synthesis. The Journal of the Acoustical Society of America 85, 2 (1989) 858–867. https://doi.org/10.1121/1.397557. [CrossRef] [PubMed] [Google Scholar]
- M. Cuevas-Rodríguez, L. Picinali, D. González-Toledo, C. Garre, E. de la Rubia-Cuestas, L. Molina-Tanco, A. Reyes-Lecuona: 3D Tune-In Toolkit: An open-source library for real-time binaural spatialisation. PLoS One 14, 3 (2019) e0211899. https://doi.org/10.1371/journal.pone.0211899. [CrossRef] [PubMed] [Google Scholar]
- M.A. Gerzon: Periphony: With-height sound reproduction. Journal of the Audio Engineering Society 21, 1 (1973) 2–10. https://www.aes.org/e-lib/browse.cfm?elib=2012. [Google Scholar]
- F. Zotter, M. Frank: Ambisonics: A practical 3D audio theory for recording, studio production, sound reinforcement, and virtual reality, in Vol. 19 of Springer Topics in Signal Processing, Springer International Publishing, Cham. 2019. https://link.springer.com/10.1007/978-3-030-17207-7. [CrossRef] [Google Scholar]
- C. Schissler, P. Stirling, R. Mehra: Efficient construction of the spatial room impulse response, in 2017 IEEE Virtual Reality (VR). 2017, pp. 122–130. https://doi.org/10.1109/VR.2017.7892239. [CrossRef] [Google Scholar]
- M. Gorzel, A. Allen, I. Kelly, J. Kammerl, A. Gungormusler, H. Yeh, F. Boland: Efficient encoding and decoding of binaural sound with resonance audio, in 2019 AES International Conference on Immersive and Interactive Audio. 2019. https://www.aes.org/e-lib/browse.cfm?elib=20446. [Google Scholar]
- B. Rafaely: Fundamentals of Spherical Array Processing, Vol. 8. Springer, 2015. https://link.springer.com/book/10.1007/978-3-662-45664-4. [CrossRef] [Google Scholar]
- A. Avni, J. Ahrens, M. Geier, S. Spors, H. Wierstorf, B. Rafaely: Spatial perception of sound fields recorded by spherical microphone arrays with varying spatial resolution. The Journal of the Acoustical Society of America 133, 5 (2013) 2711–2721. https://doi.org/10.1121/1.4795780. [CrossRef] [PubMed] [Google Scholar]
- A. McKeag, D.S. McGrath: Sound field format to binaural decoder with head tracking, in AES Convention 6r. 1996. https://www.aes.org/e-lib/browse.cfm?elib=7477. [Google Scholar]
- B. Bernschütz, A.V. Giner, C. Pörschmann, J. Arend: Binaural reproduction of plane waves with reduced modal order, Acta Acustica United with Acustica 100, 5 (2014) 972–983. https://doi.org/10.3813/AAA.918777. [CrossRef] [Google Scholar]
- C. Schörkhuber, M. Zaunschirm, R. Höldrich: Binaural Rendering of Ambisonic Signals via Magnitude Least Squares, in Fortschritte Der Akustik-DAGA 2018, Munich, Germany. 2018, pp. 339–342. https://www.researchgate.net/publication/325080691_Binaural_Rendering_of_Ambisonic_Signals_via_Magnitude_Least_Squares. [Google Scholar]
- Z. Ben-Hur, J. Sheaffer, B. Rafaely: Joint sampling theory and subjective investigation of plane-wave and spherical harmonics formulations for binaural reproduction. Applied Acoustics 134 (2018) 138–144. https://doi.org/10.1016/j.apacoust.2018.01.016. [CrossRef] [Google Scholar]
- F. Brinkmann, A. Lindau, S. Weinzierl, S. van de Par, M. Müller-Trapet, R. Opdam, M. Vorländer: A high resolution and full-spherical head-related transfer function database for different head-above-torso orientations. Journal of the Audio Engineering Society 65, 10 (2017) 841–848. https://www.aes.org/e-lib/browse.cfm?elib=19357. [CrossRef] [Google Scholar]
- C. Guezenoc, R. Seguier: HRTF individualization: A survey, in AES Convention 145. 2018. https://www.aes.org/e-lib/browse.cfm?elib=19855. [Google Scholar]
- C. Pörschmann, J.M. Arend, F. Brinkmann: Directional equalization of sparse head-related transfer function sets for spatial upsampling. IEEE/ACM Transactions on Audio, Speech, and Language Processing 27, 6 (2019) 1060–1071. https://doi.org/10.1109/TASLP.2019.2908057. [CrossRef] [Google Scholar]
- Z. Ben-Hur, D.L. Alon, R. Mehra, B. Rafaely: Efficient representation and sparse sampling of head-related transfer functions using phase-correction based on ear alignment. IEEE/ACM Transactions on Audio, Speech, and Language Processing 27, 12 (2019) 2249–2262. https://doi.org/10.1109/TASLP.2019.2945479. [CrossRef] [Google Scholar]
- Z. Ben-Hur, D.L. Alon, B. Rafaely, R. Mehra: Loudness stability of binaural sound with spherical harmonic representation of sparse head-related transfer functions. EURASIP Journal on Audio, Speech, and Music Processing 2019, 1 (2019) 5. https://doi.org/10.1186/s13636-019-0148-x. [CrossRef] [Google Scholar]
- B. Bernschütz: Microphone arrays and sound field decomposition for dynamic binaural recording. Doctoral Thesis, Technische Universitüt Berlin, Berlin, 2016. https://doi.org/10.14279/depositonce-5082. [Google Scholar]
- T. Lübeck: Perceptual evaluation of mitigation approaches of errors due to spatial undersampling, in Binaural renderings of spherical microphone array data, Master Thesis, Chalmers University of Technology. 2019. https://www.hdl.handle.net/20.500.12380/300268. [Google Scholar]
- T. Lübeck, J.M. Arend, C. Pӧrschmann, H. Helmholz, J. Ahrens: Perceptual evaluation of mitigation approaches of impairments due to spatial undersampling in binaural rendering of spherical microphone array data: Dry acoustic environments, in International Conference on Digital Audio Effects 2020, Vienna. 2020. https://www.researchgate.net/publication/345020177_Perceptual_Evaluation_of_Mitigation_Approaches_of_Impairments_due_to_Spatial_Undersampling_in_Binaural_Rendering_of_Spherical_Microphone_Array_Data_Dry_Acoustic_Environments. [Google Scholar]
- T. McKenzie, D. Murphy, G. Kearney: An evaluation of preprocessing techniques for virtual loudspeaker binaural ambisonic rendering, in EAA Spatial Audio Signal Processing Symposium, Paris, France. 2019, pp. 149–154. https://doi.org/10.25836/sasp.2019.09. [Google Scholar]
- Z. Ben-Hur, D. Alon, R. Mehra, B. Rafaely: Binaural reproduction using bilateral Ambisonics, in 2020 AES international Conference on Audio for Virtual and Augmented Reality. 2020. https://www.aes.org/e-lib/browse.cfm?elib=20871. [Google Scholar]
- Z. Ben-Hur, D.L. Alon, R. Mehra, B. Rafaely: Binaural reproduction based on bilateral Ambisonics and ear-aligned HRTFs. IEEE/ACM Transactions on Audio, Speech, and Language Processing 29 (2021) 901–913. https://doi.org/10.1109/TASLP.2021.3055038. [Google Scholar]
- F. Brinkmann, S. Weinzierl: Comparison of head-related transfer functions pre-processing techniques for spherical harmonics decomposition, in 2018 AES International Conference on Audio for Virtual and Augmented Reality. 2018. https://www.aes.org/e-lib/browse.cfm?elib=19683. [Google Scholar]
- P. Majdak, C. Hollomey, R. Baumgartner: AMT 1.x: A toolbox for reproducible research in auditory modeling. Submitted to Acta Acustica (2021). [Google Scholar]
- J. Reijniers, D. Vanderelst, C. Jin, S. Carlile, H. Peremans: An ideal-observer model of human sound localization. Biological Cybernetics 108, 2 (2014) 169–181. https://doi.org/10.1007/s00422-014-0588-4. [CrossRef] [PubMed] [Google Scholar]
- R. Baumgartner, P. Majdak: Decision making in auditory externalization perception: Model predictions for static conditions. Acta Acustica 5 (2021) 59. https://doi.org/10.1051/aacus/2021053. [CrossRef] [EDP Sciences] [Google Scholar]
- S. Jelfs, J.F. Culling, M. Lavandier: Revision and validation of a binaural model for speech intelligibility in noise. Hearing Research 275, 1 (2011) 96–104. https://doi.org/10.1016/j.heares.2010.12.005. [CrossRef] [PubMed] [Google Scholar]
- I. Engel: BinauralSH library for Matlab [Code]. Zenodo. 2021. https://doi.org/10.5281/zenodo.4633933. [Google Scholar]
- L. McCormack, S. Delikaris-Manias: Parametric first-order ambisonic decoding for headphones utilising the cross-pattern coherence algorithm, in EAA Spatial Audio Signal Processing Symposium, Paris, France. 2019, pp. 173–178. https://doi.org/10.25836/sasp.2019.26. [Google Scholar]
- Z. Ben-Hur, F. Brinkmann, J. Sheaffer, S. Weinzierl, B. Rafaely: Spectral equalization in binaural signals represented by order-truncated spherical harmonics. The Journal of the Acoustical Society of America 141, 6 (2017) 4087–4096. https://doi.org/10.1121/1.4983652. [CrossRef] [PubMed] [Google Scholar]
- O. Kirkeby, P.A. Nelson: Digital Filter Design for Inversion Problems in Sound Reproduction. Journal of the Audio Engineering Society 47, 7/8 (1999) 583–595. https://www.aes.org/e-lib/browse.cfm?elib=12098. [Google Scholar]
- I. Engel, D.L. Alon, P.W. Robinson, R. Mehra: The effect of generic headphone compensation on binaural renderings, in 2019 AES International Conference on Immersive and Interactive Audio. 2019. https://www.aes.org/e-lib/browse.cfm?elib=20387. [Google Scholar]
- I. Engel, D. Alon, K. Scheumann, R. Mehra: Listener preferred headphone frequency response for stereo and spatial audio content, in 2020 AES International Conference on Audio for Virtual and Augmented Reality. 2020. https://www.aes.org/e-lib/browse.cfm?elib=20868. [Google Scholar]
- C. Hold, H. Gamper, V. Pulkki, N. Raghuvanshi, I.J. Tashev: Improving binaural Ambisonics decoding by spherical harmonics domain tapering and coloration compensation, in ICASSP 2019 – 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). 2019, pp. 261–265. https://doi.org/10.1109/ICASSP.2019.8683751. [Google Scholar]
- J. Daniel, J.-B. Rault, J.-D. Polack: Ambisonics encoding of other audio formats for multiple listening conditions, in AES Convention 105. 1998. https://www.aes.org/e-lib/browse.cfm?elib=8385. [Google Scholar]
- M.A. Gerzon: General metatheory of auditory localisation, in AES Convention 92. 1992. https://www.aes.org/e-lib/browse.cfm?elib=6827. [Google Scholar]
- T. McKenzie, D.T. Murphy, G. Kearney: Diffuse-field equalisation of binaural ambisonic rendering. Applied Sciences 8, 10 (2018) 1956. https://doi.org/10.3390/app8101956. [CrossRef] [Google Scholar]
- M.J. Evans, J.A.S. Angus, A.I. Tew: Analyzing head related transfer function measurements using surface spherical harmonics. The Journal of the Acoustical Society of America 104, 4 (1998) 2400–2411. https://doi.org/10.1121/1.423749. [CrossRef] [Google Scholar]
- J.M. Arend, F. Brinkmann, C. Pӧrschmann: Assessing spherical harmonics interpolation of time-aligned head-related transfer functions. Journal of the Audio Engineering Society 69, 1/2 (2021) 104–117. https://www.aes.org/e-lib/browse.cfm?elib=21019. [CrossRef] [Google Scholar]
- M. Zaunschirm, C. Schӧrkhuber, R. Hӧldrich: Binaural rendering of Ambisonic signals by head-related impulse response time alignment and a diffuseness constraint. The Journal of the Acoustical Society of America 143, 6 (2018) 3616–3627. https://doi.org/10.1121/1.5040489. [CrossRef] [PubMed] [Google Scholar]
- L. Rayleigh: XII. On our perception of sound direction. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 13, 74 (1907) 214–232. https://doi.org/10.1080/14786440709463595. [CrossRef] [Google Scholar]
- J. Vilkamo, T. Bäckstrӧm, A. Kuntz: Optimized covariance domain framework for time-frequency processing of spatial audio. Journal of the Audio Engineering Society 61, 6 (2013) 403–411. https://www.aes.org/e-lib/browse.cfm?elib=16831. [Google Scholar]
- I. Engel, D.F.M. Goodman, L. Picinali: Improving Binaural Rendering with Bilateral Ambisonics and MagLS, in Fortschritte Der Akustik-DAGA 2021, Vienna, Austria. 2021, pp. 1608–1611. https://www.researchgate.net/publication/355773450_Improving_Binaural_Rendering_with_Bilateral_Ambisonics_and_MagLS. [Google Scholar]
- M. Noisternig, A. Sontacchi, T. Musil, R. Holdrich: A 3D Ambisonic based binaural sound reproduction system, in 24th AES International Conference: Multichannel Audio, The New Reality. 2003. https://www.aes.org/e-lib/browse.cfm?elib=12314. [Google Scholar]
- I. Engel, C. Henry, S.V. Amengual Garí, P.W. Robinson, D. Poirier-Quinot, L. Picinali: Perceptual comparison of Ambisonics-based reverberation methods in binaural listening, in EAA Spatial Audio Signal Processing Symposium, Paris, France. 2019, pp. 121–126. https://doi.org/10.25836/sasp.2019.11. [Google Scholar]
- A.H. Stroud, D. Secrest: Gaussian Quadrature Formulas. Prentice-Hall, 1966. [Google Scholar]
- V.I. Lebedev: Spherical quadrature formulas exact to orders 25–29. Siberian Mathematical Journal 18, 1 (1977) 99–107. https://doi.org/10.1007/BF00966954. [CrossRef] [Google Scholar]
- R.H. Hardin, N.J.A. Sloane: McLaren’s improved snub cube and other new spherical designs in three dimensions. Discrete & Computational Geometry 15, 4 (1996) 429–441. https://doi.org/10.1007/BF02711518. [Google Scholar]
- B. Bernschütz, C. Pӧrschmann, S. Spors, S. Weinzierl: SOFiA Sound Field Analysis Toolbox, in Proceedings of the International Conference on Spatial Audio (ICSA), Detmold, Germany. 2011. http://audiogroup.web.th-koeln.de/PUBLIKATIONEN/Bernschuetz_ICSA2011.pdf. [Google Scholar]
- B. Bernschütz: A spherical far field HRIR/HRTF compilation of the Neumann KU 100, in Proceedings of the 40th Italian (AIA) Annual Conference on Acoustics and the 39th German Annual Conference on Acoustics (DAGA). 2013, pp. 592–595. https://audiogroup.web.th-koeln.de/FILES/AIA-DAGA2013_HRIRs.pdf. [Google Scholar]
- R. Baumgartner, P. Majdak, B. Laback: Modeling soundsource localization in sagittal planes for human listeners. The Journal of the Acoustical Society of America 136, 2 (2014) 791. https://doi.org/10.1121/1.4887447. [CrossRef] [PubMed] [Google Scholar]
- B.F.G. Katz, M. Noisternig: A comparative study of interaural time delay estimation methods. The Journal of the Acoustical Society of America 135, 6 (2014) 3530–3540. https://doi.org/10.1121/1.4875714. [CrossRef] [PubMed] [Google Scholar]
- T. McKenzie, D. Murphy, G. Kearney: Interaural level difference optimisation of first-order binaural Ambisonic rendering, in 2019 AES International Conference on Immersive and Interactive Audio. 2019. https://www.aes.org/e-lib/browse.cfm?elib=20421. [Google Scholar]
- T. Leclère, M. Lavandier, F. Perrin: On the externalization of sound sources with headphones without reference to a real source. The Journal of the Acoustical Society of America 146, 4 (2019) 2309–2320. https://doi.org/10.1121/1.5128325. [CrossRef] [PubMed] [Google Scholar]
- C. Armstrong, T. McKenzie, D. Murphy, G. Kearney: A perceptual spectral difference model for binaural signals, in AES Convention 145. 2018. https://www.aes.org/e-lib/browse.cfm?elib=19722. [Google Scholar]
- B.R. Glasberg, B.C.J. Moore: Derivation of auditory filter shapes from notched-noise data. Hearing Research 47, 1 (1990) 103–138. https://doi.org/10.1016/0378-5955(90)90170-T. [CrossRef] [PubMed] [Google Scholar]
- R. Barumerli, P. Majdak, J. Reijniers, R. Baumgartner, M. Geronazzo, F. Avanzini: Predicting directional sound-localization of human listeners in both horizontal and vertical dimensions, in AES Convention 148. 2020. https://www.aes.org/e-lib/browse.cfm?elib=20777. [Google Scholar]
- T. May, S. van de Par, A. Kohlrausch: A probabilistic model for robust localization based on a binaural auditory front-end. IEEE Transactions on Audio, Speech, and Language Processing 19, 1 (2011) 1–13. https://doi.org/10.1109/TASL.2010.2042128. [CrossRef] [Google Scholar]
- P. Majdak, M.J. Goupell, B. Laback: 3-D localization of virtual sound sources: Effects of visual environment, pointing method, and training. Attention, Perception, & Psychophysics 72, 2 (2010) 454–469. https://doi.org/10.3758/APP.72.2.454. [CrossRef] [PubMed] [Google Scholar]
- S. Werner, F. Klein, T. Mayenfels, K. Brandenburg: A summary on acoustic room divergence and its effect on externalization of auditory events, in 2016 Eighth International Conference on Quality of Multimedia Experience (QoMEX). 2016, pp. 1–6. https://doi.org/10.1109/QoMEX.2016.7498973. [Google Scholar]
- V. Best, R. Baumgartner, M. Lavandier, P. Majdak, N. Kopčo: Sound externalization: A review of recent research. Trends in Hearing 24 (2020). https://doi.org/10.1177/2331216520948390. [CrossRef] [Google Scholar]
- S. Klockgether, S. van de Par: Just noticeable differences of spatial cues in echoic and anechoic acoustical environments. The Journal of the Acoustical Society of America 140, 4 (2016) EL352–EL357. https://doi.org/10.1121/1.4964844. [CrossRef] [PubMed] [Google Scholar]
- I. Engel, D.F.M. Goodman, L. Picinali: Supplementary material for “Assessing HRTF preprocessing methods for Ambisonics rendering through perceptual models” [Dataset]. Zenodo. 2021. https://doi.org/10.5281/zenodo.5806405. [Google Scholar]
- J. Sheaffer, B. Rafaely: Equalization strategies for binaural room impulse response rendering using spherical arrays, in 2014 IEEE 28th Convention of Electrical Electronics Engineers in Israel (IEEEI). 2014, pp. 1–5. https://doi.org/10.1109/EEEI.2014.7005804. [Google Scholar]
- H. Lee, M. Frank, F. Zotter: Spatial and timbral fidelities of binaural Ambisonics decoders for main microphone array recordings, in 2019 AES International Conference on Immersive and Interactive Audio. 2019. https://www.aes.org/e-lib/browse.cfm?elib=2039. [Google Scholar]
- I. Engel, C. Henry, S.V. Amengual Garí, P.W. Robinson, L. Picinali: Perceptual implications of different Ambisonics based methods for binaural reverberation. The Journal of the Acoustical Society of America 149, 2 (2021) 895–910. https://doi.org/10.1121/10.0003437. [CrossRef] [PubMed] [Google Scholar]
- T. Lübeck, C. Pӧrschmann, J.M. Arend: Perception of direct sound, early reflections, and reverberation in auralizations of sparsely measured binaural room impulse responses, in 2020 AES International Conference on Audio for Virtual and Augmented Reality. 2020. https://www.aes.org/e-lib/browse.cfm?elib=20865. [Google Scholar]
- AMT Team: The Auditory Modeling Toolbox full package (version 1.1.0) [code]. https://sourceforge.net/projects/amtoolbox/files/AMT%201.x/amtoolbox-full-1.1.0.zip/download. [Google Scholar]
- B. Rafaely, A. Avni: Interaural cross correlation in a sound field represented by spherical harmonics. The Journal of the Acoustical Society of America 127, 2 (2010) 823–828. https://doi.org/10.1121/1.3278605. [CrossRef] [PubMed] [Google Scholar]
- E.G. Williams: Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography. Academic Press, 1999. [Google Scholar]
- M. Poletti: Unified description of ambisonics using real and complex spherical harmonics, in Proc. Ambisonics Symp. 2009. https://web.iaem.at/ambisonics/symposium2009/proceedings/ambisym09-poletti-realandcomplexsh.pdf. [Google Scholar]
- C. Andersson: Headphone Auralization of Acoustic Spaces Recorded with Spherical Microphone Arrays. Master Thesis, Chalmers University of Technology, 2016. https://www.hdl.handle.net/20.500.12380/247969. [Google Scholar]
Cite this article as: Engel I. Goodman D.F.M. & Picinali L. 2022. Assessing HRTF preprocessing methods for Ambisonics rendering through perceptual models. Acta Acustica, 6, 4.
All Tables
All Figures
 |
Figure 1 SH spectra of the FABIAN HRTF [13]: (a) before preprocessing, (b) after time alignment through phase correction by ear alignment [16], and (c) after setting its phase to zero. The b90 and b99 parameters are shown, indicating the lowest spatial order that contains 90% and 99%, respectively, of the HRTF’s energy for a particular frequency bin [16]. The SH spectrum is defined as the energy of the SH-HRTF’s coefficients at every order n, according to Eq. (A.8) in the Appendix. |
| In the text | |
 |
Figure 2 Absolute HRTF magnitude errors (left ear) and interaural phase delay errors, averaged across 110 directions in an approximate Lebedev grid. HRTFs were interpolated from truncated SH-HRTFs (Trunc method) for five different spatial orders (1, 10, 20, 30, 44). The dotted lines indicate an approximation of the just noticeable differences: 1 dB for magnitude and 20 μs for phase delay. |
| In the text | |
 |
Figure 3 Top: Interaural time differences (ITD) and interaural level differences (ILD), plotted as a function of azimuth on the horizontal plane for the same HRTFs evaluated in Figure 2. Bottom: violin plots showing the absolute ITD and ILD errors for each HRTF on the horizontal plane, where the horizontal dotted lines represent the approximate JNDs in anechoic conditions, according to Klockgether and van de Par [63], and the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
| In the text | |
 |
Figure 4 (a) Absolute HRTF magnitude (left ear) and (b) interaural phase delay errors, averaged across 110 directions in an approximate Lebedev grid. HRTFs were preprocessed with the nine methods at N = 3 and interpolated. The horizontal dotted lines indicate an approximation of the just noticeable differences: 1 dB for magnitude and 20 μs for phase delay. The vertical dashed line indicates the aliasing frequency. |
| In the text | |
 |
Figure 5 Top: Interaural time differences (ITD) and interaural level differences (ILD), plotted as a function of azimuth on the horizontal plane for HRTFs preprocessed with the nine methods at N = 3 and interpolated. Bottom: violin plots showing the absolute ITD and ILD errors for each HRTF on the horizontal plane, where the dotted lines represent the approximate JNDs in anechoic conditions, according to Klockgether and van de Par [63], and the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
| In the text | |
 |
Figure 6 Top: Estimated loudness, which was chosen as a perceptually-motivated representation of the magnitude, of the left-ear HRTF. The top-left plot shows the Reference (original HRTF) and the other plots show HRTFs preprocessed with the nine methods at N = 3 and interpolated over all available directions (11 950). Bottom: violin plots showing the PSD between each method and the reference for the approximate 110-point Lebedev grid (lower is better), where the vertical dashed lines indicate that the groups on the left are significantly different (p < 0.05) than the groups on the right. |
| In the text | |
 |
Figure 7 Binaural models’ output for HRTFs that were preprocessed with different methods and interpolated for spatial orders 1 to 44. Top left: left-ear perceptual spectral difference (PSD [56]) with the reference, averaged across the approximate 110-point Lebedev grid (lower is better). Top middle and top right: lateral and polar localisation precision, as estimated by the model of Reijniers et al. [26] for the same 110 directions (lower is better). Bottom left: externalisation, as estimated by the model of Baumgartner and Majdak [27] for 180 median plane directions (higher is better). Bottom right: spatial release from masking (SRM) in dB, as estimated by the model of Jelfs et al. [28], averaged for 180 masker positions in the horizontal plane. Reference data (black dotted line) was obtained from the original HRTF. Detailed data in tabular form is provided in [64]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.