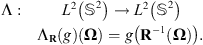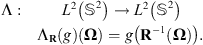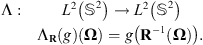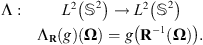| Issue |
Acta Acust.
Volume 7, 2023
Topical Issue - CFA 2022
|
|
|---|---|---|
| Article Number | 40 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.1051/aacus/2023033 | |
| Published online | 14 August 2023 | |
Scientific Article
Spherical correlation as a similarity measure for 3-D radiation patterns of musical instruments
1
STMS Lab – IRCAM, CNRS, Sorbonne Université, Ministère de la Culture, Paris, France
2
City, University of London, Northampton Square, EC1V 0HB London, UK
* Corresponding author: thibaut.carpentier@ircam.fr
Received:
8
November
2022
Accepted:
26
June
2023
We investigate the use of spherical cross-correlation as a similarity measure of sound radiation patterns, with potential applications for their study, organization, and manipulation. This work is motivated by the application of corpus-based synthesis techniques to spatial projection based on the radiation patterns of orchestral instruments. To this end, we wish to derive spatial descriptors to complement other audio features available for the organization of the sample corpus. Considering two directivity functions on the sphere, their spherical correlation can be computed from their spherical harmonic coefficients. In addition, one can search for the 3-D rotation matrix which maximizes the cross-correlation, i.e. which offers the optimal spherical shape matching. The mathematical foundations of these tools are well established in the literature; however, their practical use in the field of acoustics remains relatively limited and challenging. As a proof of concept, we apply these techniques both to simulated radiation data and to measurements derived from an existing database of 3-D directivity patterns of orchestral instruments. Using these examples we present several test cases to compare the results of spherical correlation to mathematical and acoustical expectations. A range of visualization methods are applied to analyze the test cases, including multi-dimensional scaling, employed as an efficient technique for data reduction and navigation. This article is an extended version of a study previously published in [Carpentier and Einbond. 16th Congrès Français d’Acoustique (CFA), Marseille, France, April 2022, pp. 1–6. https://openaccess.city.ac.uk/id/eprint/28202/].
Key words: Radiation patterns / Spherical acoustics / Rotational matching
© The Author(s), Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The directivity properties of sound sources, in particular musical instruments and voices, have been shown to be a key factor in the perception of acoustical sources in a reverberant environment [2, 3], for the reproduction of sound by electroacoustic devices [4, 5], and for the realistic synthesis of sources in auralization and virtual acoustic frameworks [6–9]. In all these areas of ongoing research, it would be beneficial to formulate a compact way to describe, compare, and classify sound radiation patterns.
Audio descriptors are widely and successfully used for the classification of musical and sonic material [10–12]. However, they are primarily evaluated on monophonic signals and therefore do not capture the complex spatial patterns of acoustical sources such as musical instruments. In order to analyze these patterns computationally, we require a similarity measure for pairwise comparisons, from which we can derive a multidimensional spatial description. The primary aim of our study is to investigate the cross-correlation of these patterns as a similarity measure and clustering tool.
1.1 Motivation
This work was initiated during an artistic-research residency where composer Aaron Einbond sought to extend corpus-based concatenative synthesis (CBCS) with spatial features. CBCS [13] is a sound synthesis method where short sound segments, or units, are automatically selected from a large database of audio samples and then assembled (i.e. concatenated) for playback. By re-arranging units from a corpus of live- or pre-recorded sounds, the technique is capable of synthesizing rich and musically expressive materials [14].
In CBCS, a unit selection algorithm is responsible for finding the sequence of units that best matches a given target specifying the sound or phrase to be synthesized. The selection is performed according to descriptors of the units, that is, feature characteristics extracted from or attributed to the source sounds. A multi-dimensional descriptor space is populated with the sound units and a distance function guides the unit selection algorithm to find the optimal sequence of units to fit the target.
Most often, the descriptors used are acoustical parameters computationally analyzed from the audio signals [15] and expected to be representative of the acoustical structure of the sound units. This typically includes temporal, spectral, harmonic, spectro-temporal, and energetic properties of the sound events, such as fundamental frequency, loudness, spectral centroid, etc. However, these descriptors do not commonly include spatial information, which would be useful especially when considering audio signals from acoustic instruments. One initial motivation for our work is to incorporate spatial descriptors into the CBCS method as a way to extend and improve our previous experiments on spatialized CBCS [16–18]. More specifically, we wish to apply CBCS to a corpus of musical instrument recordings, taking their radiation patterns into account as supplemental descriptors for the organization of the database.
1.2 Previous work
To incorporate radiation patterns in the context of CBCS, as described above, requires a rigorous comparison, or distance function between patterns. However, radiation patterns are in essence multidimensional data, and comparing them is therefore not an obvious task.
One way to assess their resemblance is by evaluating their spatial correlation, defined as follows. A cross-correlation coefficient is a frequency-dependent scalar value that expresses the similarity between sound pressures at two given positions in space [19]. This coefficient can then be integrated over the entire discrete set of measurement sensors for two radiation functions: the result is their spatial correlation. Looking chronologically at examples of this technique, Moreau [20, 21] employs such a spatial correlation for the qualitative assessment of a directivity model of spherical microphone arrays against measured data. Pollow [22] (Sects. 3.3.1–3.3.5) uses spatial correlation for the analysis of instrumental radiation patterns from the Technical University of Berlin (TU Berlin), discussed in further detail below. He produces scatter plots of the correlation values of partial tones radiated by the instruments, similar to what we present in Section 5 using a different algorithm. Sridhar et al. [23] use spatial correlation to compare polar responses of different loudspeakers and assess their invariance over a specified frequency range.
However, spatial correlation presents disadvantages that motivated us to pursue a more flexible and efficient method based on spherical harmonics. As radiation patterns are acoustic wave fields evaluated on the surface of a sphere, they can be conveniently represented by their spherical harmonic coefficients, using a decomposition of the angular functions into the orthonormal set of spherical harmonics [24]. This representation has already proven useful for the analysis [5], reproduction [9], interpolation [25], extrapolation [26], or auralization [27] of directivity functions.
The spherical harmonic representation can also be used to evaluate the correlation of two signals on the sphere; this will be referred to as spherical correlation. Spherical correlation offers some advantages over spatial correlation as presented above: (a) it is independent of the acquisition setup, i.e. from the number and positions of measurement microphones; this potentially allows for comparisons of data from different origins. (b) As spherical harmonic expansions can be easily rotated, spherical correlation can be used to determine the angular displacement (or lag) needed to align the two signals on the sphere. This is widely used in the field of image processing in order to perform 3-D shape-matching, also known as shape registration [28–33]. (c) As spherical harmonic expansion offers the most compact representation of radiation data for a given resolution, spherical correlation can be computed efficiently.
The spherical correlation formalism is discussed in depth in the mathematical literature. The state of the art is introduced in [34], building on the foundation of the spatial Fourier transform [35]. However, while “conventional” correlation is ubiquitous for the analysis of audio signals, so far the practical use of spherical correlation in the field of acoustics remains relatively limited and challenging.
In a chronological review of acoustics applications, spherical correlation is briefly presented in [5, 36], but actually unused. It is used by Guillon [37, 38] to compute similarities between spatial frequency response surfaces (SFRS), and later to clusterize a dataset of SFRS; by Deboy and Zotter [39] to perform rotational tracking of a moving trumpet, for which they address the question of discretizing the 3-D rotation group; and by Pollow et al. [26] to measure the quality of range extrapolation of head-related transfer functions, independent of a possible gain mismatch. In a recent publication, Pezzoli et al. [40] propose a set of metrics, including the spherical correlation coefficient, to compare the sound radiation of several historical violins. Similar to our study, Hohl and Zotter [41] use spherical correlation as a similarity measure of radiation patterns of musical instruments. They examine whether different partials at the same frequency, but originating from different played pitches, exhibit similar radiation on a given instrument. This is promising work, but their short paper does not provide much detail.
1.3 Source data and methods
Our study is both motivated and facilitated by the availability of existing datasets of radiation patterns of orchestral instruments and voices that have been obtained by previous researchers. These studies use acoustical measurements, in anechoic conditions, with surrounding circular or spherical microphone arrays. Instruments are excited either by human players or, in some cases, by electromechanical devices such as an artificial mouth for brass instruments. Many authors have reported such measurements either using synchronous multichannel recordings [3, 6, 42–52] or repeating the signals and rotating the instrument [48, 49, 53–57]. In the case of a human player or singer, the reproducibility of the signals is of course a matter of concern.
Throughout this article, we use a database published by TU Berlin [50, 58] that constitutes, to date, one of the most comprehensive datasets of publicly available 3-D high-resolution synchronous measurements, with radiation patterns for 41 modern and historical orchestral instruments.
In the following sections, we review the theory of spherical correlation and expand on the studies reviewed above to present applications to the analysis of directivity functions. We argue that the spherical correlation coefficient, as a simple scalar number, is a powerful tool for the comparison and similarity measurement of radiation patterns. After introducing the mathematical preliminaries (Sect. 2), we discuss practical considerations for an actual implementation, in particular with respect to the discretization of the search space for rotational matching (Sect. 3). In Section 4, we present numerical simulations to elicit basic properties of spherical correlation and to validate our implementation. We then present several visualization techniques, based on a matrix of cross-correlation values, that can be helpful to detect similarities among radiation patterns, and we propose the use of multidimensional scaling to clusterize radiation data. We apply these tools to several case studies of measured directivity data of musical instruments (Sect. 5), and we show that spherical correlation, both with and without rotational matching, can unveil interesting radiation similarities across frequencies or partials of a given instrument, or across multiple instruments.
2 Theoretical background
2.1 Cross-correlation on the sphere
Given two shapes f and g, we wish to find the find the rotation that best aligns them. Let f be a square-integrable function on the unit sphere  . In the simple case, let us assume that g is a rotated version of f, i.e. f = ΛR(g) for some 3-D rotation R. We denote ΛR the rotational operator defined such that
. In the simple case, let us assume that g is a rotated version of f, i.e. f = ΛR(g) for some 3-D rotation R. We denote ΛR the rotational operator defined such that 
We wish to find the rotation R. In the more general case, given the two patterns f and g, we wish to find the rotation that best aligns the two shapes on the sphere. This can be accomplished by evaluating the cross-correlation between the two functions
and finding the rotation R that maximizes the above integral [34]. However, evaluating CR(f, g) for all possible rotations in the spatial domain is a time-consuming task. Instead, we undertake it in the spatial Fourier domain. Since f and g are square-integrable on the sphere  , we can write their Fourier expansions [35]
, we can write their Fourier expansions [35]
 are the spherical harmonic functions, and
are the spherical harmonic functions, and  are the Fourier coefficients of f. Here we have further assumed that f and g are bandlimited, with their bandwidth B = (N + 1), N being the maximum order of the Fourier expansion.
are the Fourier coefficients of f. Here we have further assumed that f and g are bandlimited, with their bandwidth B = (N + 1), N being the maximum order of the Fourier expansion.
A well-known property of the conventional (Euclidian) Fourier transform is that a translation in the time domain is interpreted as a phase shift in the frequency domain. For the Fourier transform on  , this property means that the magnitudes of the Fourier coefficients are invariant under rotation: writing fn(Ω) for the nth frequency component of f,
, this property means that the magnitudes of the Fourier coefficients are invariant under rotation: writing fn(Ω) for the nth frequency component of f,
the quantity |fn(Ω)| is invariant under rotation.
Furthermore, the spherical harmonic basis functions of each order  transform among themselves under rotation according to
transform among themselves under rotation according to
where  is the Wigner-D function (see Appendix). Equation (5) is valid for complex-valued spherical harmonics. When considering real-valued spherical harmonics (as typically used in the field of Ambisonics research), a similar result holds, however involving the Wigner-d function instead of Wigner-D; details can be found for instance in [59] (Eqs. (16)–(20)).
is the Wigner-D function (see Appendix). Equation (5) is valid for complex-valued spherical harmonics. When considering real-valued spherical harmonics (as typically used in the field of Ambisonics research), a similar result holds, however involving the Wigner-d function instead of Wigner-D; details can be found for instance in [59] (Eqs. (16)–(20)).
Now, using equations (3)–(5), it is possible to simplify equation (2) into:
A complete demonstration can be found for instance in [34]. Equation (6) allows us efficiently to compute the cross-correlation by combining the Fourier coefficients of f and g. From this, we can now search for which rotation R maximizes CR(f, g).
In equations (5) and (6), the Fourier coefficients are rotated by means of the explicit formulae with the Wigner-D functions (or Wigner-d for real-valued harmonics); in our practical implementation, we rather use recurrence relations as this appears to be computationally more efficient and numerically stable [60–62].
2.2 Normalized cross-correlation
The normalized cross-correlation [31, 38, 63] is simply a variant of equation (2) normalized by the energy of f and g, written
The numerator of this expression has already been developed in equation (6). The denominator can be easily calculated thanks to Parseval’s identity:
As expressed above, the cross-correlation coefficient  corresponds to a cosine similarity measure. It is also possible to construct a Pearson correlation coefficient by replacing f and g with
corresponds to a cosine similarity measure. It is also possible to construct a Pearson correlation coefficient by replacing f and g with  and ğ, where
and ğ, where  results from centering f on its spatial average. In the spherical harmonic domain, the spatial average is simply given by the 0th-order component
results from centering f on its spatial average. In the spherical harmonic domain, the spatial average is simply given by the 0th-order component  . This approach is used, for example, in [37, 38, 40]. In [64], this is also referred to as the normalized cross-covariance coefficient.
. This approach is used, for example, in [37, 38, 40]. In [64], this is also referred to as the normalized cross-covariance coefficient.
3 Finding the optimal rotation R
A rotation in  can be equivalently represented by: (a) a 3 × 3 rotation matrix, (b) a set of 3 Euler angles (or alternatively 3 Tait–Bryan angles), (c) a unit quaternion, also known as a versor, or (d) an axis–angle representation (i.e. a unit vector indicating the direction of an axis of rotation, and an angle describing the magnitude of the rotation about the axis). The different properties of these formalisms – such as compactness, numerical stability, computational cost, singularity or gimbal lock, etc. – can easily be found in the literature, as well as conversion formulae from one representation to another [65–67].
can be equivalently represented by: (a) a 3 × 3 rotation matrix, (b) a set of 3 Euler angles (or alternatively 3 Tait–Bryan angles), (c) a unit quaternion, also known as a versor, or (d) an axis–angle representation (i.e. a unit vector indicating the direction of an axis of rotation, and an angle describing the magnitude of the rotation about the axis). The different properties of these formalisms – such as compactness, numerical stability, computational cost, singularity or gimbal lock, etc. – can easily be found in the literature, as well as conversion formulae from one representation to another [65–67].
We denote as SO(3) the 3-D rotation group, also known as the special orthogonal group. SO(3) contains all rotations R about the origin in 3-D Euclidean space:  and det(R) = +1}, where I3 is the 3 × 3 identity matrix. In other words, SO(3) is the subgroup of orthogonal matrices with determinant +1.
and det(R) = +1}, where I3 is the 3 × 3 identity matrix. In other words, SO(3) is the subgroup of orthogonal matrices with determinant +1.
We must explore the SO(3) space in order to determine the rotation R ∈ SO(3) that maximizes equation (6) or (7) correlation. One possibility would be to use a gradient descent technique, which has been formalized on the SO(3) rotation group in [68, 69]. However, we have decided not to use this approach, as it presents several challenges: the procedure requires approximation of the directional derivatives, with an adjustable small step size, in order to converge to the nearest local maximum. It might also be necessary to restart the algorithm from several initial values, and choosing the optimal step size or the initial value is not a trivial task. Therefore, in the scope of this paper, we instead proceed with a sampling-based exploration of the SO(3) space, as this is conceptually simpler and straightforward in its implementation.
3.1 Sampling the rotation group SO(3)
Due to the topology of SO(3), different choices of parametrization may yield distributions of samples with various properties or biases. To implement our approach, we would prefer a uniform and deterministic sampling scheme. The definition of uniform is subject to interpretation, but essentially the sampling grid should ensure both global coverage and local separation. Note that sampling the SO(3) space is not the same task as uniformly distributing samples on the sphere  , which is a well-studied question in the field of spherical acoustics processing [70]. In contrast, the SO(3) sampling problem is examined for instance in [71–74]. While an extensive analysis is beyond the scope of this article, in the following subsections we discuss and evaluate the most relevant approaches.
, which is a well-studied question in the field of spherical acoustics processing [70]. In contrast, the SO(3) sampling problem is examined for instance in [71–74]. While an extensive analysis is beyond the scope of this article, in the following subsections we discuss and evaluate the most relevant approaches.
3.1.1 Parametrization by Euler angles
For the sake of simplicity, we will follow [34, 37] and use regular sampling in terms of ZYZ Euler angles (α, β, γ):
with 0 ≤ j, k < 2B. According to [34], this sampling scheme is suitable for the analysis of band-limited functions with bandwidth B. In this case, the size of the search space is 2B × 2B × 2B.
Note that the null rotation (α = β = γ = 0) is not part of the sampling grid. Consequently, correlating a signal with itself will not yield α = β = γ = 0, but rather β = π/(4B). This is counter-intuitive but not problematic. To circumvent this, it has been proposed [37] first to rotate one of the patterns, f or g, by −π/(4B) around the y axis.
We should also note that the true rotation R might not be on the sampling grid. Therefore, we might only find an approximate solution  that should be close to R. The notion of distance in SO(3) will be discussed in Section 3.1.4.
that should be close to R. The notion of distance in SO(3) will be discussed in Section 3.1.4.
3.1.2 Sampling by Halton sequences
Another sampling strategy is proposed in [74], extending and improving a probabilistic approach first proposed in [75, 76] with the use of Halton sequences in the unit cube. This approach is easy to implement, and allows the generation of sampling grids with arbitrary numbers of samples.
3.1.3 Axis-angle visualization
Any 3-D rotation can be represented by an axis-angle representation. This formalism is useful for visualizing the projective space in  [72]: each rotation is drawn as a vector with direction n (the axis of the rotation) and a magnitude corresponding to ϑ (the rotation angle). In Figure 1, we present several sampling grids generated via (a) Euler parametrization, (b) Halton sequences, or (c) the Hopf fibration sampling proposed in [72]. The later is another, more elaborated, deterministic strategy that produces dense and highly uniform grids. It can be observed graphically in Figure 1 that Euler sampling is not perfectly uniform, while the Hopf fibration grid divides the surface of SO(3) into regions of (apparently) equal volume. However, the Hopf fibration approach is restricted to fixed sequences of samples, i.e. it cannot generate an arbitrary number of samples. Therefore, for the remainder of this article, we will use the basic Euler sampling (Eq. (9)) for its simplicity and scalability (with respect to B).
[72]: each rotation is drawn as a vector with direction n (the axis of the rotation) and a magnitude corresponding to ϑ (the rotation angle). In Figure 1, we present several sampling grids generated via (a) Euler parametrization, (b) Halton sequences, or (c) the Hopf fibration sampling proposed in [72]. The later is another, more elaborated, deterministic strategy that produces dense and highly uniform grids. It can be observed graphically in Figure 1 that Euler sampling is not perfectly uniform, while the Hopf fibration grid divides the surface of SO(3) into regions of (apparently) equal volume. However, the Hopf fibration approach is restricted to fixed sequences of samples, i.e. it cannot generate an arbitrary number of samples. Therefore, for the remainder of this article, we will use the basic Euler sampling (Eq. (9)) for its simplicity and scalability (with respect to B).
 |
Figure 1 Visualization of SO(3) sampling grids using the axis-angle representation. The color represents the magnitude ϑ of the rotation (from blue to red). (a) Regular sampling of Euler angles (as in Eq. (9)) with B = 4, leading to (2B)3 = 512 samples; (b) Uniform distribution using Halton sequences [74] with 512 sampling points; (c) Uniform incremental sampling using the Hopf fibration [72] with 576 sampling points. |
3.1.4 Distance measure on SO(3)
Various functions for measuring the “closeness” between 3-D rotations have been proposed in the literature. The usual (angular) distance between two rotation matrices R, Q ∈ SO(3) is given by [39, 71, 77] 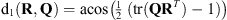 . This metric measures the angle of rotation needed to map the transformation R to the transformation Q, or equivalently the angle of rotation associated to the transformation QR−1. Alternatively, we can interpret d1(R, Q) as a scaled Froebenius norm, since
. This metric measures the angle of rotation needed to map the transformation R to the transformation Q, or equivalently the angle of rotation associated to the transformation QR−1. Alternatively, we can interpret d1(R, Q) as a scaled Froebenius norm, since  , where
, where  is the Frobenius norm defined as
is the Frobenius norm defined as  . Several other distance functions have also been proposed, producing values in different ranges and of different units. Huynh [78] presents a detailed review and analysis of various metrics, and demonstrates that many of them are functionally equivalent. Huynh concludes that the following metric, based on quaternions, is both spatially and computationally more efficient:
. Several other distance functions have also been proposed, producing values in different ranges and of different units. Huynh [78] presents a detailed review and analysis of various metrics, and demonstrates that many of them are functionally equivalent. Huynh concludes that the following metric, based on quaternions, is both spatially and computationally more efficient:
where qR is the unit quaternion corresponding to matrix R, and · denotes the quaternion inner product (scalar inner product of two 4-D unit vectors). Equation (10) gives values in the range [0, 1], with 0 denoting that R and Q are close [73, 78]. This metric will be used for the remainder of this article.
Note that, while a distance metric in SO(3) is useful, it must be handled with care in the context of this paper: consider for example an axis-symmetric pattern f, for example a cardioid in the y direction. Rotate f around the z-axis with R0 ≡ (α0, β0, γ0) = (π, 0, 0). Rotate f around the x-axis with R1 ≡ (α1, β1, γ1) = (0, 0, π). Both scenarios result in the exact same pattern g; however, the two rotations differ, and their distance is d(R0, R1) = 1.
4 Numerical simulations
We run numerical simulations on simple test cases in order to elicit basic properties of spherical correlation and to validate our implementation.
4.1 Impact of SO(3) sampling
As discussed above (Sect. 3.1), the choice of the sampling grid for SO(3) might have an influence on the accuracy and efficiency of the maximization problem equation (7) correlation. For the sake of simplicity, here we consider only the regular Euler sampling of equation (9). However, we investigate the use of oversampling i.e. we use a smaller step size in discretizing the Euler angles (α, β, γ). Instead of using 2B samples for each parameter, we use  . This seems relevant as our scenario involves directional functions with relatively low bandwidth (B = 5 if we consider the radiation patterns available in the TU Berlin database) compared to other authors (Kostelec [34] typically presents results with B = 128 or B = 256). With such low bandwidth (B = 5), the angular step size is very large (π/B = 36°), and therefore high angular misalignment might occur. Of course, oversampling the search grid results in higher computation time, but that is not the focus of this paper.
. This seems relevant as our scenario involves directional functions with relatively low bandwidth (B = 5 if we consider the radiation patterns available in the TU Berlin database) compared to other authors (Kostelec [34] typically presents results with B = 128 or B = 256). With such low bandwidth (B = 5), the angular step size is very large (π/B = 36°), and therefore high angular misalignment might occur. Of course, oversampling the search grid results in higher computation time, but that is not the focus of this paper.
We run the following numerical simulation: (a) generate a random directional function f with a given bandwidth B; (b) generate a random rotation matrix [79] R ∈ SO(3) and compute g = ΛR(f), a rotated version of f; (c) sample SO(3) and search for the rotation matrix  that maximizes the cross-correlation; (d) compute the cross-correlation after rotational matching, i.e. the cross-correlation between g and
that maximizes the cross-correlation; (d) compute the cross-correlation after rotational matching, i.e. the cross-correlation between g and  ; (e) repeat the simulation for various samplings of SO(3), varying the oversampling factor
; (e) repeat the simulation for various samplings of SO(3), varying the oversampling factor  ; (f) repeat the simulation for various bandwidths 1 ≤ B ≤ 6. For each test case, we perform 10,000 Monte-Carlo runs. The results are presented in Figure 2.
; (f) repeat the simulation for various bandwidths 1 ≤ B ≤ 6. For each test case, we perform 10,000 Monte-Carlo runs. The results are presented in Figure 2.
 |
Figure 2 Impact of oversampling the SO(3) search space. |
For each simulated bandwidth B, it can be observed that oversampling the search space improves accuracy, allowing for a higher cross-correlation (closer to 1), and a smaller distance (closer to 0) between the expected and estimated rotation matrices. For B = 2, the distance criteria  appears bounded: this is due to the non-uniqueness of the solution, as several matrices
appears bounded: this is due to the non-uniqueness of the solution, as several matrices  achieve rotational matching (with normalized cross-correlation values close to 1), while being “far” from the expected/simulated matrix R (see concluding remark in Sect. 3.1.4).
achieve rotational matching (with normalized cross-correlation values close to 1), while being “far” from the expected/simulated matrix R (see concluding remark in Sect. 3.1.4).
As a result of this simulation, we speculate that sufficiently oversampled Euler schemes yield accuracy comparable to other highly uniform grids (such as Halton sequences or Hopf fibration).
4.2 Auto-correlation of elementary patterns
We now perform a simulation to highlight some basic properties of the spherical auto-correlation, i.e. the correlation  of a signal f with a rotated copy of itself. For f we use different elementary functions (see legend of Fig. 3). For the sake of simplicity and visualization, we examine rotations only around the yaw angle: R ≡ R(α). Figure 3 presents the auto-correlation as a function of the rotational lag α.
of a signal f with a rotated copy of itself. For f we use different elementary functions (see legend of Fig. 3). For the sake of simplicity and visualization, we examine rotations only around the yaw angle: R ≡ R(α). Figure 3 presents the auto-correlation as a function of the rotational lag α.
 |
Figure 3 Top: polar pattern of elementary functions. Bottom: auto-correlation of f as a function of the rotational lag α (yaw angle). Columns (a) to (e): |
We can make a few simple observations in agreement with theoretical expectations: (1) the auto-correlation coefficient  varies in range [−1; 1]; (2) as the omnidirectional pattern
varies in range [−1; 1]; (2) as the omnidirectional pattern 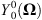 is rotationally invariant, its auto-correlation always equals 1; (3) as all examples of f are real functions, the auto-correlation is an even function of α; (4) the auto-correlation reaches its peak at the origin (α = 0), and for any lag α we have:
is rotationally invariant, its auto-correlation always equals 1; (3) as all examples of f are real functions, the auto-correlation is an even function of α; (4) the auto-correlation reaches its peak at the origin (α = 0), and for any lag α we have:  ; (5) the auto-correlation of a periodic function is, itself, periodic with the same period; (6) the Dirac distribution is an eigenfunction of the auto-correlation function, i.e. the auto-correlation of a Dirac delta is a Dirac distribution itself. All of these are well-known properties of the auto-correlation function of time signals, here pertained to spherical auto-correlation of directional signals on
; (5) the auto-correlation of a periodic function is, itself, periodic with the same period; (6) the Dirac distribution is an eigenfunction of the auto-correlation function, i.e. the auto-correlation of a Dirac delta is a Dirac distribution itself. All of these are well-known properties of the auto-correlation function of time signals, here pertained to spherical auto-correlation of directional signals on  .
.
4.3 Comparing two patterns of different shapes
So far, we have assumed that the two patterns f and g are rotated cousins and therefore have the same bandwidth. In the most general case, we are interested in comparing two arbitrary radiation patterns, potentially with different bandwidths. Such a scenario generally yields  , but the rotational alignment can still be effective.
, but the rotational alignment can still be effective.
As a proof of concept, we investigate the cross-correlation function of two patterns f and g having different “shapes”. For f, we choose an Nth-order Dirac delta, i.e. a maximally directional pattern in direction Ω0:
For g, we build a “directionally reduced” version of  such as:
such as:
where ζ ∈ [0–100] is a directivity (or “aperture”) factor, and wn(ζ) is a spherical harmonics weighting function. The precise choice of wn(ζ) is not relevant here; we simply build a weighting function that allows us to generate a series of patterns with significantly different characteristics. We further impose that ζ = 100% produces a Dirac delta, and ζ = 0% produces an omnidirectional pattern. In other words, wn(ζ) is used to simulate patterns with varying bandwidths (see Fig. 4). Techniques for building such weighting functions have been proposed e.g. in [80]. Finally, we rotate g with a random matrix R ∈ SO(3), repeating the simulation with 10,000 Monte-Carlo runs. One example of resulting rotational alignment is presented in Figure 5.
 |
Figure 4 Polar representation of angular pattern g(Ω) for N = 4 and for various values of the directivity factor ζ. The radial scale is linear. |
 |
Figure 5 Example of rotational alignment of two patterns with different bandwidths. In magenta, the original pattern f (Dirac delta with N = 4); in black, the rotated and directionally reduced pattern g (with ζ = 40%); in red, pattern f after rotational alignment with the estimated matrix |
In Figure 6, we present the cross-correlation of the functions f and g for varying values of ζ. As expected, we observe that the spherical correlation coefficient decreases when ζ tends towards 0, i.e. when g becomes more omnidirectional. When ζ = 0%, the correlation value is not 0, but the curve is bounded by 0.2. Indeed, when g reduces to the omnidirectional pattern, it is easy to show that ∀f:
 |
Figure 6 Numerical simulation of correlation between Dirac delta f and directionally reduced g, as a function of the directivity factor ζ, for N = 4. Top: Normalized cross-correlation (after rotational matching) between f and g. Bottom: Distance |
When f is a Dirac delta, this further simplifies to  , which equals 0.2 in our example. The actual shape of the
, which equals 0.2 in our example. The actual shape of the  curve (Fig. 6) depends on the chosen weighting functions wn(ζ). Similarly, the distance between the estimated and expected rotation matrix significantly increases as ζ gets smaller.
curve (Fig. 6) depends on the chosen weighting functions wn(ζ). Similarly, the distance between the estimated and expected rotation matrix significantly increases as ζ gets smaller.
These results suggest that the spherical correlation coefficient can be a relevant indicator of similarity between patterns of different shapes/bandwidth. As with any correlation measure, this essentially allows for qualitative interpretation; a quantitative analysis of the correlation coefficient depends on the context and purposes.
5 Application to measured data
We now apply the approaches presented in the previous sections to measured data. As mentioned in the introduction, our source is the acoustic instrumental radiation database, containing 41 modern and historical orchestral instruments, made available by TU Berlin [50, 58]. This database contains single-tone recordings at two dynamic levels (pp and ff). For our processing, we use the ff data due to its better signal-to-noise ratio.
In the TU Berlin database, radiation patterns were measured by a surrounding spherical array of 32 microphones with a radius of 2.1 m. The database is published with spherical harmonic coefficients calculated for the first 10 partials of each played note, and third-octave band-averaged patterns are also provided [81]. Methods to obtain the spherical harmonic coefficients from such measurements are not discussed here; readers can refer e.g. to [5, 9, 24, 36, 54]. In our work, we directly exploit the precomputed spherical harmonic coefficients for the order N = 4 (25 coefficients) as provided by the TU database authors. An acoustic source centering algorithm [82, 83] has also been applied, by the TU researchers, to these spherical harmonic coefficients (below 1 kHz) in order to align the acoustic center of the sound source to the geometrical center of the microphone array, and to account for the resulting phase shifts at the microphone positions. This source re-alignment procedure is known to be particularly important for directivity functions that model the complex sound pressure (as is the case in the TU database), with significant impact on the spherical harmonic coefficients; when only the absolute values (sound pressure levels) are considered, the impact of displaced sources might be less severe [84, 85]. The TU database includes both uncentered and centered data, and we have used the latter to minimize the influence on our calculations of changes to instrument alignment. The practical setup used in the collection of the TU data exhibits a spatial aliasing frequency of approximately 1.1 kHz [58, 82]. Observations made above this frequency should therefore be interpreted cautiously.
Finally, let us emphasize that our aim in this section is not to provide a thorough analysis of the TU database, but rather to exemplify the qualitative results that can potentially be obtained through spherical correlation. More in-depth discussions about the TU data can be found e.g. in [22, 58, 86–88].
5.1 Similarities over frequencies
In Figure 7, we propose scatter plots to visualize the matrix of cross-correlation values, i.e. the normalized cross-correlation of all pairs of partial tones of a given instrument, for four different instruments. The color code depicts the magnitude of the correlation coefficient (its absolute value), from blue (low correlation) to red (high correlation). The x and y axes represent the frequency on a logarithmic scale. The size of the scatter dots is slightly adjusted with frequency in order to avoid overlapping dots and to improve readability. This visualization is similar to what is proposed in [22, 89]. Such a diagram allows the compact combination of a significant amount of information: the number of dots is equal to (Np × Nt)2 where Nt is the number of played tones and Np the number of partials for each tone. In the TU dataset, Np = 10. As the matrix of cross-correlation values is persymmetric, so is the scatter diagram. The cross-correlation values presented here have been calculated without rotational alignment. When applying rotational alignment, the scatter diagrams (not shown here) do not exhibit significant differences, suggesting the musicians did not rotate dramatically during the recording session.
 |
Figure 7 Matrix of cross-correlation values for all recorded tones, including all partials, organized by frequency. Results are presented for clarinet in B♭, cello, tuba, and double bass. |
Inspecting these diagrams, as well as those of other instruments not displayed here for brevity, we can draw several general observations. The results are consistent with the categorization of the TU database into three groups of instruments, as proposed by Shabtai et al. [58]: those with one expected radiation point, such as brass instruments; those with several expected radiation points, such as woodwind instruments, with sound radiated by the bell, the fingering holes, and the mouthpiece; and those with a full body radiating sound, such as string instruments. For brass instruments (tuba in Fig. 7), the cross-correlation values vary slowly with frequency, and the diagonal in the matrix has a wide “spread”. This suggests that the radiation patterns evolve smoothly over frequency. In other words, nearby frequencies produce similar directivity patterns. For woodwind instruments (clarinet in Fig. 7), there is greater correlation of all partials for low frequencies, approximately below 300 Hz. With increasing frequencies, the correlation values exhibit abrupt changes, manifested by vertical and horizontal “stripes” and “clusters” in the depicted matrix containing the cross-correlation values. These discontinuities are likely related to changes of fingering, for example using the register key. For string instruments (cello and double bass in Fig. 7), the cross-correlation is relatively large in the low frequency region (for wavelengths larger than the dimensions of the instrument), but drops sharply at higher frequencies, suggesting greater variations in their radiation patterns. For further interpretations see e.g. [22, 46, 89].
5.2 Similarities over partials
Following an idea from Hohl and Zotter [41, 46], we now plot the matrix of cross-correlations organized by partials rather than by frequencies. In other words, we generate a 2-D color-coded diagram, similar to the one presented in the previous section, but with x and y axes now organized by partial tones instead of frequencies. The matrix is organized in blocks each containing a chromatic scale, with each successive block representing a different partial for each played note. Black dashed lines separate each partial index, for ease of readability. This sorting makes the comparison of cross-correlation between partials more evident. With this matrix arrangement, partials with matching frequency are located on the secondary diagonals. Figure 8 illustrates examples of results for the same four instruments as in Figure 7.
 |
Figure 8 Matrix of cross-correlation values (for all partial tones of one chromatic scale), organized by partial tones. |
For the tuba, it can be observed that most partials at the same frequency exhibit strongly correlated radiation, regardless of the played pitch from which they originate. This is in line with the observations made in Section 5.1. Similar results can be observed for other brass instruments (not shown here). For the clarinet, however, the diagram is less regular. Along the diagonal, a checkered pattern appears, revealing that partial tones with similar or nearby frequencies radiate differently. More precisely, pitches from C to G# are strongly correlated, but differ significantly from pitches A to B. The abrupt change between these two blocks corresponds to the transition between the first and second registers of the B♭ clarinet. This suggests that the addition of the register key, and consequently discontinuous change in fingerings, strongly impacts the radiation pattern. For string instruments such as the cello and double bass, except for a few narrow diagonal red lines, the overall similarities between partials are low. Each partial seems to have its own radiation pattern, uncorrelated with the other partials, suggesting that the directivities of these instruments are rather complex. The diagrams presented in Figure 8 are qualitatively comparable to ones obtained by Hohl and Zotter with another database of instrument recordings. Further analysis can be found in [41, 46].
5.3 Visualization with multidimensional scaling
Another motivation for this work is to classify the TU Berlin database for subsequent manipulation with corpus-based synthesis techniques: by organizing instrumental samples according to their directional characteristics, the resulting low-dimensional representation can be used, along with other audio descriptors, to navigate the sample corpus. With an approach to pairwise spherical correlation in place, we can now examine applications to classify and navigate larger collections of 3-D radiation patterns by using multidimensional scaling (MDS) [90]. MDS is used to translate information about the pairwise distances (or dissimilarities) among a set of p objects into a configuration of p points mapped onto an abstract Cartesian space. MDS is therefore a means of visualizing the level of similarity of samples within a dataset.
We apply MDS analysis, using a dimensionality of 2 for simplicity of visualization and interpretation, to measured radiation patterns of different instruments for the fundamental frequency of various played pitches. Examples of MDS for two different pitches are presented as scatter plots in Figure 9. The color code corresponds to the three categories of instruments cited above [58]: in red, instruments with one expected radiation point such as brass; in blue, instruments with several expected radiation points, such as woodwinds; and in black, instruments with a complex radiation pattern, such as strings. The MDS plots for these two pitches, as well as for others not shown for brevity, show groupings among instruments of these three categories. Further sub-classes of instruments of similar construction appear to cluster together: for example, the cylindrical-bore brass instruments in the trombone family, which are separated from conical-bore French horn and tuba. Members of the single-reed clarinet and saxophone families cluster together, as do members of the double-reed bassoon and dulcian family. As expected, historical instruments are positioned near their modern counterparts. Therefore we observe that MDS based on spherical correlation allows us efficiently to segregate and organize the instruments in accordance with their predicted categories.
 |
Figure 9 2D MDS map of radiation patterns of the pitches B3 (a) and E3 (b) for various brass (red), woodwind (blue), and string instruments (black). |
The examples presented in Figure 9 were evaluated with pitches performed at dynamic ff. When both dynamic levels pp and ff are included in the MDS analysis, the corresponding points (not shown for clarity) are mapped closely in the MDS space, indicating that the played dynamic level does not substantially affect the clustering operation.
Rotational matching has not been applied to these examples in order better to visualize the distinctions between instrument categories – as, by definition, rotational alignment always yields higher correlations. We examine the effects of rotational matching in the following section.
5.4 Exploring rotational matches
We now show that rotational matching can be a convenient tool to explore the database further and search for similarities, regardless of the orientation of the instruments. The following analyses refer to the radiation coefficients averaged over third-octave bands [58]. While both pp and ff dynamics have been analyzed, the results are presented only for ff data for the sake of readability.
5.4.1 Across instruments
In Figure 10, we examine the cross-correlation between all instruments in a single frequency band, before and after applying rotational matching. The axes are organized according to the expected three main categories of radiation characteristics, separated by black lines (“brass-like”, “woodwind-like”, and “string-like”, as discussed in Sect. 5.3). Within each category, instruments are presented in alphabetical order without presupposing any finer categorization. White spaces indicate instruments for which no data is present in the chosen frequency band (timpani, flutes, and oboes in Fig. 10). As the matrix of cross-correlation values is persymmetric, only half of it is shown: instead, in the upper and lower triangles we present the correlation values with and without rotational alignment, respectively.
 |
Figure 10 Matrix of cross-correlation values between instruments for the third-octave band centered at 198 Hz. Lower triangle: without rotational matching; Upper triangle: after rotational matching. |
We can make a number of observations, ranging from more general to more specific:
The upper triangle has higher values than the lower triangle, by definition of rotational matching.
In the upper triangle, nearly all correlation values are greater than 0.5, indicating some degree of similarities across most instruments. This is somewhat expected: in this relatively low frequency band, most instruments have energy concentrated in the lower spherical harmonic orders, and they behave roughly like first-order functions, with cardioid- or dipole-like patterns. The concentration of energy within the lower orders is also, partly, a consequence of the acoustic centering process that has been applied [82].
The three “diagonal blocks”, representing correlation among instruments of the same category, show overall higher correlation than the other blocks, comparing instruments of unlike categories. This is observed both before and after rotational matching, but with several nuances: for example, the “brass-like” instruments show a particularly large increase in correlation after rotational matching, which is consistent with the assumption that they each have a single point of radiation but oriented in different directions. To a lesser extent, the “string-like” instruments show a significant improvement in correlation following rotational matching, which again fits the observation that several of these instruments feature a similar construction but oriented in different directions (for example violin, viola, cello, and guitar). In these cases, therefore, the similarities among instruments are most clearly revealed when they are rotated.
A few instruments visually emerge as “outliers”, exhibiting a line (vertical or horizontal) with strikingly low correlation values, both with and without rotational matching. In particular, this is the case for the double action harp, pedal timpani, French horn, and to a lesser extent dulcian. Indeed, it appears that these instruments have significant energy in higher orders (N > 1), and consequently their radiation patterns are dissimilar to other instruments. We can propose several hypothetical explanations: (a) These instruments are also outliers in terms of their construction and performance technique, with few obvious correlates in the database: the timpani and harp are percussion instruments that are only provisionally grouped with “strings” due to their full-body radiation. The horn, while technically a brass instrument, has historically been acknowledged as an exceptional member of that group due to its timbre and directivity [2]: it is the only instrument whose bell is oriented behind the performer, with the performer’s hand mediating the output. Its directional characteristic is therefore expected to be more complex (of higher order) than other brass instruments performed with open bells. While the dulcian may be expected to correlate with other members of the bassoon family, it is an outlier as the oldest instrument of the database by nearly a century (ca. 1600) [50] and we hypothesize that its unusual directivity is consistent with historical trends favoring more focused directivity as instruments have modernized. (b) Consistent with these observations, the presence of higher order components may be caused by the contribution of large, spatially extended, excitation sources (i.e. the absence of a unique natural acoustic center) and/or by off-center sound sources and aliasing errors; this seems especially plausible for the harp and timpani, as they are among the largest instruments in the database. We hypothesize that the performance of the centering algorithm might be degraded for these instruments (in spite of the relatively low frequency). (c) When measuring harp and timpani, “a relatively small-area floor was used” to support the instrument [83]; for the wavelength of interest, this might have contributed to undesired reflections or scattering (based on the available pictures, this floor was covered with absorptive materials for the timpani only). (d) Finally, the timpani are unique in the database as only one played pitch was recorded for each (historical and modern); this could explain differences from the other instruments, due to relatively fewer data for the third-octave averaging.
As already noted in Section 5.3, modern instruments and their historical counterparts usually exhibit high correlation values, even without rotational matching. The best rotational alignment is typically achieved with a relatively small angular displacement (not shown here for brevity), suggesting that the difference between modern and historical instruments might be essentially due to slight changes in the performer’s orientation and instrument construction. It is, however, not obvious why modern and historical viola exhibit low correlation values in this particular frequency band.
Double bass exhibits only moderate correlation with other members of the string quartet; this bias is possibly an effect of its large size relative to the frequency band being considered: we have noted in Section 5.1 that, for string instruments, partial tones within a small frequency interval show low correlation values for wavelengths smaller than the size of the instrument; consequently, the averaged directivity pattern of Double bass in the frequency band centered at 198 Hz is questionable.
While it is surprising there is not higher correlation between French horn and natural horn, the latter may be anomalous because relatively few performed pitches in the natural harmonic scale leave sparse data for third-octave averaging in this register (similar to timpani as mentioned above).
We observe high correlation between several unexpected pairs of instruments before rotational matching, such as trumpet and historical violin, tuba and historical violin, or trumpet and clarinet. There is not space to analyze every example in this paper; however, spherical correlation and the proposed visualization strategies appear as promising tools for further research. For brevity we also have not systematically discussed here the specific angle of rotation that produces the optimal rotational alignment; again, this would be a fruitful topic for further study.
5.4.2 Across frequencies
As mentioned in observation 3, rotational alignment is especially relevant for brass, so we will focus on the tenor trombone as one particular representative. Still considering its data in the 198 Hz-centered band, we present in Figure 11 its cross-correlation with all other instruments in all available frequency bands.
 |
Figure 11 Matrix of cross-correlation values between tenor trombone in the third-octave band centered at 198 Hz, and all available instruments. (a) Without rotational matching; (b) After rotational matching. |
Before rotational matching, we observe high correlation values with the other trombones at the same frequency (historical tenor trombone, modern and historical bass trombone), but also with the bass trombone in nearby frequency bands (99 Hz and 157 Hz). This expected affinity between all trombones in nearby frequencies is further increased after applying rotational alignment. There is also some correlation with the trumpet in the 314 Hz band, where the shift to higher frequencies could be reasonably explained by the trumpet’s smaller dimensions.
Rotational matching additionally reveals high similarities with certain woodwind instruments, such as the bass clarinet and bassoons, in slightly lower frequency regions. In Figure 11b, the highest correlation values (≥0.95) are observed for: bass trombone (99 Hz and 198 Hz), bassoon (79 Hz), contrabassoon (63 Hz), bass clarinet (99 Hz), and historical bass trombone (99 Hz).
The three instruments that “benefit” the most from rotational alignment are contrabassoon, bass clarinet, and historical bass trombone. One hypothesis is that these instruments have a relatively similar size, but are performed with their bells oriented in different directions: the trombone points forwards in front of the performer, while the bassoon and contrabassoon bells point upwards, and the bass clarinet bell is located at the bottom of the instrument but pointing upwards. This is partially confirmed by Shabtai et al. [58] (Figs. 8a and 9a) in their measurements of acoustic source centers, where they observe that both trombone and bassoon have strong excitation sources at their bells, but with different spatial orientations. Therefore it is plausible that a suitable rotation would produce a high correlation between the radiation patterns of these instruments.
More surprisingly, there is also noticeable correlation, before and after rotational matching, with a few strings instruments (violas, basses, historical cello, and acoustic guitar) in certain frequency bands. As in Section 5.4.2, observation 2, this could be due to the relatively low-order radiation patterns of all instruments in low frequency bands.
In summary, beyond the expected correlations with other brass, Figure 11 reveals that rotational matching can capture less obvious similarities with different instrument categories, such as some woodwinds and strings, in different frequency regions. Nevertheless, a much more systematic study would be required to confidently relate these observations to the instruments’ construction and performance technique.
Now focusing on one of the above examples, in Figure 12 we graphically represent the radiation patterns for tenor trombone and contrabassoon in the respective frequency bands centered at 198 Hz and 63 Hz, where rotational alignment induced a large increase in cross-correlation. As the normalized cross-correlation is used here, it is possible to detect similarities regardless of differences in overall energies of the two instruments, as already noted by Pollow [22] (Sect. 2.3.7). The contrabassoon radiation pattern shown in Figure 12c is essentially a vertical dipole, consistent with the vertical orientation of the instrument, as compared to the horizontal orientation of the trombone. However, after rotating the contrabassoon radiation pattern, in Figure 12f we can observe that the 2-D polar patterns align nicely. This is not always the case: indeed, maximizing the 3-D shape alignment does not necessarily imply strong similarity on the horizontal plane.
 |
Figure 12 Example of 3-D rotational matching. (a) and (b): tenor trombone for the third-octave band centered at 198 Hz. (c) and (d): contrabassoon for the third-octave band centered at 63 Hz. (e): contrabassoon after rotational matching. (f) black curve: tenor trombone; similar to (b). (f) solid red curve: contrabassoon after rotational matching. (f) dashed red curve: similar to solid curve, scaled to match the overall energy of the tenor trombone. Left: visualization of sound pressure (in dB) on the sphere. Right: restriction to the horizontal plane (radial scale is in dB). |
Beyond acoustical analysis, such high correlations suggest clear applications from an artistic perspective in the case of CBCS, as discussed in the introduction. By concatenating instrumental samples according to spherical correlation, smooth transitions can be made between radiation characteristics of disparate instruments, with or without rotational alignment, suggesting a novel approach to corpus-based spatial sound synthesis.
6 Conclusion
In this paper, we discussed the use of cross-correlation on the sphere as a similarity measure for the classification of 3-D radiation patterns. We showed that this tool can facilitate thorough analysis of directivity pattern similarities across partials of one instrument or between different instruments. We have presented several visualization tools that allow the compact organization and examination of multidimensional data, revealing or confirming the radiation behavior or categorization of instruments. Multidimensional scaling, in particular, appears to be a powerful approach to clusterize instruments based on their radiation characteristics, with potential applications to the creative exploration of the corpus. We have also discussed some challenges regarding the implementation of rotational alignment, and demonstrated that rotational matching can be useful to detect similarities among different categories of instruments, or different frequency bands, by mitigating the effects of differing instrument construction and orientation.
As a consequence, spherical correlation presents promising possibilities for human or machine navigation of a database of radiation patterns. We have already applied CBCS to computer improvisation based on audio features, in particular using timbral descriptors to structure sequences of complex sounds with an audio oracle algorithm [91]. These CBCS sequences can be synthesized spatially using spherical harmonic coefficients derived from the TU database [18] and projected with a compact spherical loudspeaker array such as the IKO [92] to approximate the dynamic radiation patterns of acoustic instruments, as implemented in Einbond’s composition Prestidigitation for percussion and 3-D electronics in 2022. A further step will be to use an MDS visualization of the TU database to train the computer improvisation agent directly on spherical correlation distances themselves, allowing for direct learning and continuation of spatial gestures.
Future work will investigate other spatial descriptors for the classification of the 3-D database of orchestral instruments as well as other metrics recently proposed in [40]. Finally, we will examine whether spherical correlation can be useful to detect or correct possible rotational misalignment of a human performer across multiple measurements, thereby improving reproducibility.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101019164 (ERC MusAI – Music and Artificial Intelligence: Building Critical Interdisciplinary Studies).
Data availability statement
The Matlab code associated with this article is available in https://github.com/tcarpent/shxcorr
Appendix
A.1 Wigner-D function
Considering Euler angles with the ZYZ convention, the rotation matrix R can be expressed as a rotation of α about the z axis, followed by a rotation β about the y axis, and finally a rotation γ about the z axis:
with:
and 0 ≤ α, γ < 2π and 0 ≤ β ≤ π. With this convention, the Wigner-D function  , required to rotate complex-valued spherical harmonics, is written
, required to rotate complex-valued spherical harmonics, is written
where  is the Wigner-d function [34, 93].
is the Wigner-d function [34, 93].
References
- T. Carpentier, A. Einbond: Spherical correlation as a similarity measure for 3D radiation patterns of musical instruments, in: 16th Congrès Français d’Acoustique (CFA), Marseille, France, April, 2022. https://openaccess.city.ac.uk/id/eprint/28202/ [Google Scholar]
- J. Meyer: Acoustics and the performance of music – manual for acousticians, audio engineers, musicians, architects and musical instruments makers, 5th edn., Springer, 2009. [Google Scholar]
- J. Pätynen, T. Lokki: Directivities of symphony orchestra instruments. Acta Acustica united with Acustica 96 (2010) 138–167. [CrossRef] [Google Scholar]
- O. Warusfel, P. Derogis, R. Caussé: Radiation synthesis with digitally controlled loudspeakers, in 103rd Convention of the Audio Engineering Society, New York, September 1997. [Google Scholar]
- F. Zotter: Analysis and synthesis of sound-radiation with spherical arrays. PhD thesis. IEM, Graz, Austria, 2009. [Google Scholar]
- F. Otondo, J.H. Rindel: The influence of the directivity of musical instruments in a room. Acta Acustica united with Acustica 90 (2004) 1178–1184. [Google Scholar]
- M. Vorländer: Auralization fundamentals of acoustics, modelling, simulation, algorithms and acoustic virtual reality, Springer, Berlin, 2008. [Google Scholar]
- L.M. Wang, M.C. Vigeant: Evaluations of output from room acoustic computer modeling and auralization due to different sound source directionalities. Applied Acoustics 69, 12 (2008) 1281–1293. [CrossRef] [Google Scholar]
- M. Noisternig, F. Zotter, B.F.G. Katz: Reconstructing sound source directivity in virtual acoustic environments, in: Y. Suzuki, D. Brungart, H. Kato, Eds. Principles and applications of spatial hearing, World Scientific Press, 2011, pp. 357–373. [CrossRef] [Google Scholar]
- G. Peeters, S. McAdams, P. Herrera: Instrument sound description in the context of MPEG-7, in: International Computer Music Conference, Berlin, Germany, 2000, pp. 166–169. [Google Scholar]
- M. Muller, D.P.W. Ellis, A. Klapuri, G. Richard: Signal processing for music analysis. IEEE Journal of Selected Topics in Signal Processing 5, 6 (2011) 1088–1110. [CrossRef] [Google Scholar]
- G. Richard, S. Sundaram, S. Narayanan: An overview on perceptually motivated audio indexing and classification. IEEE 101, 9 (2013) 1939–1954. [CrossRef] [Google Scholar]
- D. Schwarz: Corpus-based concatenative synthesis. IEEE Signal Processing Magazine 24, 2 (2007) 92–104. [CrossRef] [Google Scholar]
- D. Schwarz, S. Britton, R. Cahen, T. Goepfer: Musical applications of real-time corpus-based concatenative synthesis, in: International Computer Music Conference (ICMC), Copenhagen, Denmark, 2007, pp. 47–50. [Google Scholar]
- G. Peeters, B.L. Giordano, P. Susini, N. Misdariis, S. McAdams: The Timbre Toolbox: Extracting audio descriptors from musical signals. Journal of the Acoustical Society of America 130, 5 (2011) 2902–2916. [CrossRef] [PubMed] [Google Scholar]
- A. Einbond, D. Schwarz: Spatializing timbre with corpus-based concatenative synthesis, in: International Computer Music Conference (ICMC), New York, NY, USA, 2010. [Google Scholar]
- A. Einbond: Mapping the klangdom live: Cartographies for piano with two performers and electronics. Computer Music Journal 41, 1 (2017) 61–75. [CrossRef] [Google Scholar]
- A. Einbond, J. Bresson, D. Schwarz, T. Carpentier: Instrumental radiation patterns as models for corpus-based spatial sound synthesis: Cosmologies for Piano and 3D Electronics In: International Computer Music Conference, Santiago, Chile, July, 2021, pp. 148–153. [Google Scholar]
- R.K. Cook, R.V. Waterhouse, R.D. Berendt, S. Edelman, M.C. Thompson: Measurement of correlation coefficients in reverberant sound fields. Journal of the Acoustical Society of America 27, 6 (1955) 1072–1077. [CrossRef] [Google Scholar]
- S. Moreau: Étude et réalisation d’outils avancés d’encodage spatial pour la technique de spatialisation sonore Higher Order Ambisonics: microphone 3D et contrôle de distance. PhD thesis, Université du Maine, 2006. [Google Scholar]
- S. Moreau, J. Daniel, S. Bertet: 3D sound field recording with higher order ambisonics – objective measurements and validation of a 4th order spherical microphone, in: 120th Convention of the Audio Engineering Society (AES), Paris, France, May 20–23, 2006. [Google Scholar]
- M. Pollow: Directivity Patterns for Room Acoustical Measurements and Simulations. PhD thesis, RWTH Aachen University, 2015. [Google Scholar]
- R. Sridhar, J.G. Tylka, E.Y. Choueiri: Generalized metrics for constant directivity. Journal of the Audio Engineering Society 67, 9 (2019) 666–678. [CrossRef] [Google Scholar]
- E.G. Williams: Fourier acoustics: sound radiation and nearfield acoustical holography. Academic Press, 1999. [Google Scholar]
- D. Ackermann, F. Brinkmann, F. Zotter, M. Kob, S. Weinzierl: Comparative evaluation of interpolation methods for the directivity of musical instruments. EURASIP Journal on Audio, Speech, and Music 36 (2021) 1–14. [Google Scholar]
- M. Pollow, K. Van Nguyen, O. Warusfel, T. Carpentier, M. Müller-Trapet, M. Vorländer, M. Noisternig: Calculation of head-related transfer functions for arbitrary field points using spherical harmonics decomposition. Acta Acustica united with Acustica 98 (2012) 72–82. [CrossRef] [Google Scholar]
- S. Pelzer, M. Pollow, M. Vorländer: Auralization of virtual orchestra using directivities of measured symphonic instruments, in: Acoustics 2012, Nantes, France, April, 2012. [Google Scholar]
- M. Kazhdan, T. Funkhouser: Harmonic 3D shape matching, in: ACM SIGGRAPH Conference Abstracts and Applications, New York, 2002, p. 191. [Google Scholar]
- M. Kazhdan, T. Funkhouser, S. Rusinkiewicz: Rotation invariant spherical harmonic representation of 3D shape descriptors. Eurographics Symposium on Geometry Processing, June, 2003, pp. 167–175. [Google Scholar]
- M. Kazhdan, T. Funkhouser, S. Rusinkiewicz: Symmetry descriptors and 3D shape matching, in: Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, New York, 2004, pp. 115–123. [Google Scholar]
- L. Sorgi, K. Daniilidis: Normalized cross-correlation for spherical images, in: T. Pajdla, J. Matas, Eds. Computer Vision – ECCV 2004, Springer, Berlin, 2004, pp. 542–553. [CrossRef] [Google Scholar]
- L. Shen, H. Huang, F. Makedon, A.J. Saykin: Efficient registration of 3D SPHARM surfaces, in: Canadian Conference on Computer and Robot Vision, Montreal, May 2007, pp. 81–88. [Google Scholar]
- B. Gutman, Y. Wang, T. Chan, P.M. Thompson, A.W. Toga, Shape registration with spherical cross correlation, in: X. Pennec Ed. 2nd Workshop on Mathematical Foundations of Computational Anatomy, New York, USA, 2008, pp. 56–67. [Google Scholar]
- P.J. Kostelec, D.N. Rockmore: FFTs on the rotation group. Journal of Fourier Analysis and Applications 14 (2008) 145–179. [CrossRef] [Google Scholar]
- J.R. Driscoll, D.M. Healy: Computing fourier transforms and convolutions on the 2-sphere. Advances in Applied Mathematics 15, 2 (1994) 202–250. [CrossRef] [Google Scholar]
- B. Rafaely: Fundamentals of spherical array processing, 2nd edn., Springer-Verlag, 2019. [CrossRef] [Google Scholar]
- P. Guillon: Individualisation des indices spectraux pour la synthèse binaurale: recherche et exploitation des similarités inter-individuelles pour l’adaptation ou la reconstruction de HRTF. PhD thesis, Université du Maine, 2009. [Google Scholar]
- P. Guillon, R. Nicol: Head-Related Transfer Function reconstruction from sparse measurements considering a priori knowledge from database analysis: a pattern recognition approach, in: 125th Convention of the Audio Engineering Society (AES), San Francisco, October, 2008. [Google Scholar]
- D. Deboy, F. Zotter: Acoustic center and orientation analysis of sound-radiation recorded with a surrounding spherical microphone array, in: 2nd International Symposium on Ambisonics and Spherical Acoustics, Paris, France, May, 2010. [Google Scholar]
- M. Pezzoli, A. Canclini, F. Antonacci, A. Sarti: A comparative analysis of the directional sound radiation of historical violins. Journal of the Acoustical Society of America 152, 1 (2022) 354–367. [CrossRef] [PubMed] [Google Scholar]
- F. Hohl, F. Zotter: Similarity of musical instrument radiation-patterns in pitch and partial, in: Fortschritte der Akustik (DAGA), Berlin, Germany, March, 2010. [Google Scholar]
- F. Otondo, J.H. Rindel, R. Causse, N. Misdariis, P. de la Cuadra: Directivity of musical instruments in a real performance situation, in: International Symposium on Musical Acoustics (ISMA), Mexico City, 2002, pp. 230–232. [Google Scholar]
- F. Otondo, J.H. Rindel: A new method for the radiation representation of musical instruments in auralizations. Acta Acustica united with Acustica 91 (2005) 902–906. [Google Scholar]
- B.F.G. Katz, C. d’Alessandro: Directivity measurement of the singing voice, in: 19th International Congress on Acoustics 2007 (ICA 2007), Madrid, Spain, 2–7 September 2007, 2007. [Google Scholar]
- M. Pollow, G. Behler, B. Masiero: Measuring directivities of natural sound sources with a spherical microphone array, in: 1st Ambisonics Symposium, Graz, Austria, June 2009. [Google Scholar]
- F. Hohl: Kugelmikrofonarray zur abstrahlungsvermessung von musikinstrumenten. Master’s thesis, IEM, Graz, Austria, 2009. [Google Scholar]
- M. Pollow, G.K. Behler, F. Schultz: Musical instrument recording for building a directivity database, in: Fortschritte der Akustik (DAGA), Berlin, Germany, March, 2010. [Google Scholar]
- K.J. Bodon, T.W. Leishman: Development, evaluation, and validation of a high-resolution directivity measurement system for live musical instruments. Journal of the Acoustical Society of America 138, 3 (2015) 1785. [CrossRef] [Google Scholar]
- K.J. Bodon: Development, evaluation, and validation of a high-resolution directivity measurement system for played musical instruments. Master’s thesis, Brigham Young University, 2016. [Google Scholar]
- S. Weinzierl, M. Vorländer, G. Behler, F. Brinkmann, H. von Coler, E. Detzner, J. Krämer, A. Lindau, M. Pollow, F. Schulz, N.R. Shabtai: A database of anechoic microphone array measurements of musical instruments – recordings, directivities, and audio features. Technical report. TU Berlin, 2017. [Google Scholar]
- M. Brandner, M. Frank, F. Zotter: DirPat – database and viewer of 2D/3D directivity patterns of sound sources and receivers, in: 144th Convention of the Audio Engineering Society (AES), Milan, Italy, May, 2018. [Google Scholar]
- M. Brandner, N. Meyer-Kahlen, M. Frank: Directivity pattern measurement of a grand piano for augmented acoustic reality, in: Fortschritte der Akustik, Hanover, March 2020. [Google Scholar]
- N.J. Eyring, T.W. Leishman, K.M. Sorensen, N.G.W. Eyring: Methods for automating multichannel directivity measurements of musical instruments in an anechoic chamber. Journal of the Acoustical Society of America 130, 4 (2011) 2399. [CrossRef] [Google Scholar]
- S.D. Bellows, T.W. Leishman: Spherical harmonic expansions of high-resolution musical instrument directivities. Proceedings of Meetings on Acoustics 35, 1 (2018) 035005. [CrossRef] [Google Scholar]
- T.W. Leishman, S.D. Bellows: Musical instrument directivity measurements. Journal of the Acoustical Society of America 146, 4 (2019) 2822. [CrossRef] [Google Scholar]
- T. Grother, M. Kob: High resolution 3D radiation measurements on the bassoon, in: International Symposium on Musical Acoustics (ISMA), Detmold, Germany, September 2019. [Google Scholar]
- T.W. Leishman, S.D. Bellows, C.M. Pincock, J.K. Whiting: High-resolution spherical directivity of live speech from a multiple-capture transfer function method. Journal of the Acoustical Society of America 149, 3 (2021) 1507–1523. [CrossRef] [PubMed] [Google Scholar]
- N.R. Shabtai, G. Behler, M. Vorländer, S. Weinzierl: Generation and analysis of an acoustic radiation pattern database for forty-one musical instruments. Journal of the Acoustical Society of America 141, 2 (2017) 1246–1256. [CrossRef] [PubMed] [Google Scholar]
- D.W. Ritchie, G.J.L. Kemp: Fast computation, rotation, and comparison of low resolution spherical harmonic molecular surfaces. Journal of Computational Chemistry 20, 4 (1999) 383–395. [CrossRef] [Google Scholar]
- J. Ivanic, K. Ruedenberg: Rotation matrices for real spherical harmonics. Direct determination by recursion. Journal of Physical Chemistry 100 (1996) 6342–6347. [CrossRef] [Google Scholar]
- C.H. Choi, J. Ivanic, M.S. Gordon, K. Ruedenberg: Rapid and stable determination of rotation matrices between spherical harmonics by direct recursion. Journal of Chemical Physics 111, 19 (1999) 8825–8831. [CrossRef] [Google Scholar]
- G. Aubert: An alternative to Wigner d-matrices for rotating real spherical harmonics. AIP Advances 3, 6 (2013) 062121. [CrossRef] [Google Scholar]
- B. Huhle, T. Schairer, W. Straßer: Normalized cross-correlation using SOFT, in: Proceeding of the International Workshop on Local and Non-Local Approximation in Image Processing, 19–21 August 2009, pp. 82–86. [Google Scholar]
- C. Anemüller, J. Herre: Calculation of directivity patterns from spherical microphone array recordings, in: Proceeding of the 147th Convention of the Audio Engineering Society, New York, NY, USA, October 2019. [Google Scholar]
- J. Diebel: Representing attitude: Euler angles, unit quaternions, and rotation vectors. Technical report, Stanford University, 2006. [Google Scholar]
- S. Sarabandi, F. Thomas: A survey on the computation of quaternions from rotation matrices. Journal of Mechanisms and Robotics 11, 2 (2019) 03. [CrossRef] [Google Scholar]
- W. Tape, C. Tape: Angle between principal axis triples. Geophysical Journal International 191, 2 (2012) 813–831. [CrossRef] [Google Scholar]
- D. Stein, E.R. Scheinerman, G.S. Chirikjian: Mathematical models of binary spherical-motion encoders. IEEE Transactions on Mechatronics 8, 2 (2003) 234–244. [CrossRef] [Google Scholar]
- G.S. Chirikjian, P.T. Kim, J.-Y. Koo, C.H. Lee: Rotational matching problems. International Journal of Computational Intelligence and Applications 4, 4 (2004) 401–416. [CrossRef] [Google Scholar]
- F. Zotter: Sampling strategies for acoustic holography/holophony on the sphere, in: 35th German Annual Conference on Acoustics (DAGA), Rotterdam, The Netherlands, March, 2009. [Google Scholar]
- J.C. Mitchell: Sampling rotation groups by successive orthogonal images. SIAM Journal on Scientific Computing 30, 1 (2008) 525–547. [CrossRef] [Google Scholar]
- A. Yershova, S. Jain, S.M. LaValle, J.C. Mitchell: Generating uniform incremental grids on SO(3) using the Hopf fibration. The International Journal of Robotics Research 29, 7 (2010) 801–812. [CrossRef] [PubMed] [Google Scholar]
- J.J. Kuffner: Effective sampling and distance metrics for 3D rigid body path planning. Proceedings of the IEEE International Conference on Robotics and Automation 4 (2004) 3993–3998. [Google Scholar]
- C. Beltrán, D. Ferizović: Approximation to uniform distribution in SO(3). Constructive Approximation 52, 2 (2020) 283–311. [CrossRef] [Google Scholar]
- P. Diaconis, M. Shahshahani: The subgroup algorithm for generating uniform random variables. Probability in the Engineering and Informational Sciences 1, 1 (1987) 15–32. [CrossRef] [Google Scholar]
- J. Arvo: Fast random rotation matrices, in: D. Kirk Ed. Graphics Gems III, Academic Press Professional, San Diego, 1992, pp. 117–120. [Google Scholar]
- R. Hielscher, J. Prestin, A. Vollrath: Fast summation of functions on the rotation group. Mathematical Geosciences 42 (2010) 773–794. [CrossRef] [Google Scholar]
- D.Q. Huynh: Metrics for 3D rotations: comparison and analysis. Journal of Mathematical Imaging and Vision 35, 2 (2009) 155–164. [CrossRef] [Google Scholar]
- J. Arvo: Random rotation matrices, in: J. Arvo, Ed. Graphics Gems II, Morgan Kaufmann, San Diego, 1991, pp. 355–356. [CrossRef] [Google Scholar]
- G. Huang, J. Chen, J. Benesty: A flexible high directivity beamformer with spherical microphone arrays. Journal of the Acoustical Society of America 143, 5 (2018) 3024–3035. [CrossRef] [PubMed] [Google Scholar]
- N. Shabtai, G. Behler, M. Vorländer: Database of musical instruments directivity pattern. Journal of the Acoustical Society of America 138, 3 (2015) 1784–1784. [CrossRef] [Google Scholar]
- I.B. Hagai, M. Pollow, M. Vorländer, B. Rafaely: Acoustic centering of sources measured by surrounding spherical microphone arrays. Journal of the Acoustical Society of America 130, 4 (2011) 2003–2015. [CrossRef] [PubMed] [Google Scholar]
- N.R. Shabtai, M. Vorländer: Acoustic centering of sources with high-order radiation patterns. Journal of the Acoustical Society of America 137, 4 (2015) 1947–1961. [CrossRef] [PubMed] [Google Scholar]
- M. Pollow, G. Behler, M. Vorländer: Post-processing and center adjustment of measured directivity data of musical instruments, in: Acoustics 2012, Nantes, France, April, 2012. [Google Scholar]
- S.D. Bellows, T.W. Leishman: Acoustic source centering of musical instrument directivities using acoustical holography. Proceedings of Meetings on Acoustics 42, 1 (2020) 055002. [CrossRef] [Google Scholar]
- A.C. Marruffo, V. Chatziioannou: A pilot study on tone-dependent directivity patterns of musical instruments, in: AES International Conference on Audio for Virtual and Augmented Reality, Redmond, WA, USA, August, 2022. [Google Scholar]
- E.A. Petersen, T. Colinot, F. Silva, V.H. Turcotte: The bassoon tonehole lattice: Links between the open and closed holes and the radiated sound spectrum. Journal of the Acoustical Society of America 150, 1 (2021) 398–409. [CrossRef] [PubMed] [Google Scholar]
- E. Accolti, J. Gimenez, M. Vorländer: Uncertainties of directivity data of musical instruments and their influence on room acoustics simulation. TechRxiv Preprint, September, 2022. https://doi.org/10.36227/techrxiv.20858596.v1 [Google Scholar]
- R. Baumgartner, E. Messner: Bachelor-arbeit: auswirkung der abstrahlcharakteristik auf die klangfarbe von querflöten und saxofonen. Master’s thesis. IEM, Graz, Austria, 2010. [Google Scholar]
- I. Borg, P.J.F. Groenen: Modern multidimensional scaling: theory and applications, 2nd edn. Springer, 2005. [Google Scholar]
- A. Einbond, D. Schwarz, R. Borghesi, N. Schnell: Introducing CatOracle: corpus-based concatenative improvisation with the audio oracle algorithm, in: International Computer Music Conference, Utrecht, 2016, pp. 141–147. [Google Scholar]
- F. Zotter, M. Zaunschirm, M. Frank, M. Kronlachner: A beamformer to play with wall reflections: the icosahedral loudspeaker. Computer Music Journal 41, 3 (2017) 50–68. [CrossRef] [Google Scholar]
- T. Risbo Fourier transform summation of Legendre series and D-functions. Journal of Geodesy 70, 7 (1996) 383–396. [CrossRef] [Google Scholar]
Cite this article as: Carpentier T. & Einbond A. 2023. Spherical correlation as a similarity measure for 3-D radiation patterns of musical instruments. Acta Acustica, 7, 40.
All Figures
 |
Figure 1 Visualization of SO(3) sampling grids using the axis-angle representation. The color represents the magnitude ϑ of the rotation (from blue to red). (a) Regular sampling of Euler angles (as in Eq. (9)) with B = 4, leading to (2B)3 = 512 samples; (b) Uniform distribution using Halton sequences [74] with 512 sampling points; (c) Uniform incremental sampling using the Hopf fibration [72] with 576 sampling points. |
| In the text | |
 |
Figure 2 Impact of oversampling the SO(3) search space. |
| In the text | |
 |
Figure 3 Top: polar pattern of elementary functions. Bottom: auto-correlation of f as a function of the rotational lag α (yaw angle). Columns (a) to (e): |
| In the text | |
 |
Figure 4 Polar representation of angular pattern g(Ω) for N = 4 and for various values of the directivity factor ζ. The radial scale is linear. |
| In the text | |
 |
Figure 5 Example of rotational alignment of two patterns with different bandwidths. In magenta, the original pattern f (Dirac delta with N = 4); in black, the rotated and directionally reduced pattern g (with ζ = 40%); in red, pattern f after rotational alignment with the estimated matrix |
| In the text | |
 |
Figure 6 Numerical simulation of correlation between Dirac delta f and directionally reduced g, as a function of the directivity factor ζ, for N = 4. Top: Normalized cross-correlation (after rotational matching) between f and g. Bottom: Distance |
| In the text | |
 |
Figure 7 Matrix of cross-correlation values for all recorded tones, including all partials, organized by frequency. Results are presented for clarinet in B♭, cello, tuba, and double bass. |
| In the text | |
 |
Figure 8 Matrix of cross-correlation values (for all partial tones of one chromatic scale), organized by partial tones. |
| In the text | |
 |
Figure 9 2D MDS map of radiation patterns of the pitches B3 (a) and E3 (b) for various brass (red), woodwind (blue), and string instruments (black). |
| In the text | |
 |
Figure 10 Matrix of cross-correlation values between instruments for the third-octave band centered at 198 Hz. Lower triangle: without rotational matching; Upper triangle: after rotational matching. |
| In the text | |
 |
Figure 11 Matrix of cross-correlation values between tenor trombone in the third-octave band centered at 198 Hz, and all available instruments. (a) Without rotational matching; (b) After rotational matching. |
| In the text | |
 |
Figure 12 Example of 3-D rotational matching. (a) and (b): tenor trombone for the third-octave band centered at 198 Hz. (c) and (d): contrabassoon for the third-octave band centered at 63 Hz. (e): contrabassoon after rotational matching. (f) black curve: tenor trombone; similar to (b). (f) solid red curve: contrabassoon after rotational matching. (f) dashed red curve: similar to solid curve, scaled to match the overall energy of the tenor trombone. Left: visualization of sound pressure (in dB) on the sphere. Right: restriction to the horizontal plane (radial scale is in dB). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.