| Issue |
Acta Acust.
Volume 8, 2024
|
|
|---|---|---|
| Article Number | 14 | |
| Number of page(s) | 12 | |
| Section | Speech | |
| DOI | https://doi.org/10.1051/aacus/2024006 | |
| Published online | 15 March 2024 | |
Scientific Article
Combining multiple sparse measurements with reference data regularization to create spherical directivities applied to voice data
Sorbonne Université, CNRS, Institute Jean le Rond d’Alembert, UMR 7190, 4 Place Jussieu, 75005 Paris, France
* Corresponding author: samuel.bellows11@gmail.com
Received:
20
December
2023
Accepted:
12
February
2024
Obtaining high-resolution, spherical phoneme-dependent directivities for voice radiation is beneficial for numerous acoustics applications. This work reports on a spherical interpolation method based on two interleaved measurements using a regularized least-squares fit with reference data. Maximizing the spherical correlation between previously reported results and measured data determines the regularization hyper-parameters to ensure physical solutions. While the resultant spherical directivity patterns show similarities to time-averaged results, distinct radiation characteristics appear, particularly in the range of 630 Hz to 2 kHz.
Key words: Voice directivity / Sound radiation / Speech acoustics / Spherical harmonic / Inverse problems
© The Author(s), Published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Voice directivity data is essential in applications such as telecommunications [1] or room acoustic design [2]. Over the decades, researchers have employed numerous measurement techniques to obtain increasingly finer resolutions approaching compatibility with standardized resolutions for loudspeakers [3] that are commonly employed in architectural acoustics simulation packages [4, 5]. Although initial efforts often employed a single moving microphone [6, 7], most modern techniques make use of rotations of microphone arrays or rotations of subjects within microphone arrays to leverage higher-resolution, spherical or partial-spherical results [8–12].
Often, the measured data is incompatible with standardized resolutions employed in applications because it is either (1) measured over an entire spherical surface but with insufficient spatial resolution or (2) measured with sufficient spatial resolution but only over a partial spherical surface. Both cases require some form of data interpolation to estimate unmeasured values. More recent works have considered interpolation methods for the former case [13, 14]; the present work reports on a method for the latter.
Researchers often apply least-squares fits to measured data for interpolating spherical directivities using spherical harmonic expansions [15]. However, when measurement constraints lead to unsampled regions, such as below the talker’s legs, a least-squares fit may lead to spurious radiation lobes in this region. Applying incorrect directional data to applications such as geometrical acoustics modeling [16] or determining optimized microphone placements [17] can lead to incorrect results. Regularized least-squares fits have been employed to handle this so-called “polar gap” problem. For example, Zotkin et al. [18] applied Tikhonov regularization to estimate spherical harmonic expansion coefficients in order to interpolate HRTF measurements with a polar gap. Analysis of L-curves [19] determined the amount of regularization. Aussal et al. [20] later applied a weighted Tikhonov regularization to HRTF interpolation using a fixed amount of regularization but over varying spherical harmonic expansion degrees. Regularized least-squares fits have also been applied to directivity measurements, such as for guitar amplifiers [21].
However, several aspects of the application of regularized least-squares fits to spherical harmonic expansions of voice directivity remain unresolved. For example, no work has directly evaluated the benefits or drawbacks of weighted and unweighted Tikhonov regularization. Additionally, while the amount of regularization determined by an L-curve may be a good initial choice, much is already known about voice radiation through previous research. If and how this data could be leveraged to determine improved weighted Tikhonov regularization or even be incorporated into the regularization remains unexplored. This work reports on the application of regularized least-squares fits to producing spherical directivities from two interleaved sparse measurements. A spherical correlation coefficient helps inform regularization parameters to ensure physically meaningful interpolation. The resultant phoneme-dependent spherical directivities show similarities with previously published phoneme-averaged results while highlighting unique radiation features of individual phonemes.
2 Methods
2.1 Measurement system
The voice directivity measurement system consisted of a rotating array in the anechoic chamber of the l’Institut de Recherche et Coordination Acoustique/Musique (IRCAM). As suggested by Figure 1, the measurement system employed 24 microphones equally spaced on a semi-circular arc. Microphone placement incorporated an azimuthal angle spacing of Δϕ = 7.5° with an initial offset from ϕ = 0° of Δϕ/2 = 3.75°. A motorized arm attached to the array enabled rotations to elevation angles ϑ from −45° to 90°. A fixed far-field microphone served as reference microphone for normalization between repeated captures of the measurement system.
 |
Figure 1 Directivity measurement system including the rotating arc, reference microphone and rotating chair. |
The rotatable chair, fixed at the array origin, allowed the subject to sit in two configurations. In the first, the talker faced the center of the array arc, while in the second, the talker faced the end of the array arc. In both configurations, lasers assisted in exactly aligning the subject’s mouth to the geometric array center. In each configuration, 14 elevation angle steps of Δϑ = 10° from −45° to 85° swept out a partial spherical region, producing a single dataset. Additional measurements at ϑ = 0° and ϑ = 90° facilitated polar-plane comparisons. Each configuration produced 336 unique measurements points, plus the polar-plane measurements. Incorporating both datasets and assuming symmetry across the median plane led to a total of 1,008 unique sampling positions over the sphere (see Fig. 2). During the measurement sequence, the talkers repeated select phonemes for several seconds, repeated twice to evaluate consistency. Additional information on the measurement system, procedure, and calibration are available in references [10, 11].
 |
Figure 2 Sampling positions produced from the front, side, and reflected side configurations. |
2.2 Computation of directivities
Because subjects cannot exactly repeat spoken passages or utterances with each measurement repetition, adequate compensation procedures must be employed. Narrowband data processing followed the same normalization procedure as used in [12]. First, under the assumption of linearity between the reference microphone signal x(t) and array microphone signal y(t), frequency-response functions (FRFs) Huv for the uth elevation angle rotation and the vth array position derived from the cross-spectral densities between the array and reference microphone Gxy,uv and the autospectral densities of the reference microphone Gxx,u as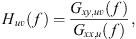 (1)where f is the frequency. The FRFs represent the ratio of signal energy at the array measurement positions relative to and correlated with the signal energy at the reference microphone. However, summation into frequency bands requires summation of radiated energies, not ratios. Consequently, a narrowband estimate of the coherent output power followed as [12]
(1)where f is the frequency. The FRFs represent the ratio of signal energy at the array measurement positions relative to and correlated with the signal energy at the reference microphone. However, summation into frequency bands requires summation of radiated energies, not ratios. Consequently, a narrowband estimate of the coherent output power followed as [12]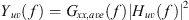 (2)where the averaged input autospectrum was
(2)where the averaged input autospectrum was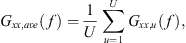 (3)with U = 24 representing the total elevation angle captures. The coherent output power represents the radiated energy at the array microphone positions using a constant input excitation equal to the average over all 24 elevation angle captures.
(3)with U = 24 representing the total elevation angle captures. The coherent output power represents the radiated energy at the array microphone positions using a constant input excitation equal to the average over all 24 elevation angle captures.
The coherence follows from the spectral estimates as (4)so that the signal-to-noise ratio (SNR) at a given frequency may be calculated as
(4)so that the signal-to-noise ratio (SNR) at a given frequency may be calculated as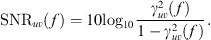 (5)
(5)
Finally, energetic summation over respective broadband ranges fb produced magnitude 1/3rd octave band directivity functions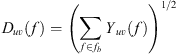 (6)with respective beam patterns Buv(f) defined as
(6)with respective beam patterns Buv(f) defined as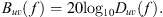 (7)
(7)
The square-root in equation (6) appears because directivity functions are not typically defined in terms of energetic quantities (see Eq. (23)).
2.3 Regularized interpolation
Spherical harmonic expansions of directivity data are commonly employed in spatial audio applications. The expansions allow data interpolation, smoothing, and compact representations. The irregularity of the combined sampling positions over the sphere and the uneven sampling density precludes the use of spherical quadrature rules and requires a least-squares fit to the data. Additionally, the sparse sampling in the region ϑ < −45° necessitates regularization to avoid spurious and non-physical radiation lobes [18, 21].
A spherical harmonic expansion of a directivity function may be expressed as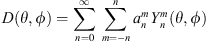 (8)where
(8)where  are the expansion coefficients, θ is the polar angle (θ = π/2 − ϑ), and
are the expansion coefficients, θ is the polar angle (θ = π/2 − ϑ), and 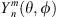 are the spherical harmonics of degree n and order m. Truncating the infinite expansion to degree N and organizing a system of equations for each of the Q sampling positions yields
are the spherical harmonics of degree n and order m. Truncating the infinite expansion to degree N and organizing a system of equations for each of the Q sampling positions yields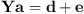 (9)where
(9)where![$$ \mathbf{Y}=\left[\begin{array}{llll}{Y}_0^0({\theta }_1,{\phi }_1)& {Y}_1^{-1}({\theta }_1,{\phi }_1)& \cdots & {Y}_N^N({\theta }_1,{\phi }_1)\\ {Y}_0^0({\theta }_2,{\phi }_2)& {Y}_1^{-1}({\theta }_2,{\phi }_2)& \cdots & {Y}_N^N({\theta }_2,{\phi }_2)\\ \vdots & \vdots & \ddots & \vdots \\ {Y}_0^0({\theta }_Q,{\phi }_Q)& {Y}_1^{-1}({\theta }_Q,{\phi }_Q)& \cdots & {Y}_N^N({\theta }_Q,{\phi }_Q)\end{array}\right], $$](/articles/aacus/full_html/2024/01/aacus230110/aacus230110-eq12.gif) (10)
(10)![$$ \mathbf{a}=\left[\begin{array}{l}{a}_0^0\\ {a}_1^{-1}\\ \vdots \\ {a}_N^N\end{array}\right], $$](/articles/aacus/full_html/2024/01/aacus230110/aacus230110-eq13.gif) (11)
(11)![$$ \mathbf{d}=\left[\begin{array}{l}D({\theta }_1,{\phi }_1)\\ D({\theta }_2,{\phi }_2)\\ \vdots \\ D({\theta }_Q,{\phi }_Q)\end{array}\right], $$](/articles/aacus/full_html/2024/01/aacus230110/aacus230110-eq14.gif) (12)and e is a Q × 1 vector containing the least-squares errors (residuals). Constructing the data vector d requires combining both datasets. However, because Gxx,ave(f) differs for the front-facing and side-facing datasets, one dataset must be normalized according to the difference in the reference microphone level between the two different measurements.
(12)and e is a Q × 1 vector containing the least-squares errors (residuals). Constructing the data vector d requires combining both datasets. However, because Gxx,ave(f) differs for the front-facing and side-facing datasets, one dataset must be normalized according to the difference in the reference microphone level between the two different measurements.
The unsampled area below the talker (polar gap) is an unconstrained region. Without regularization, the least-squares fit that minimizes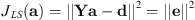 (13)will attempt to reduce errors at the Q sampling positions with no regard to the expansion in the unconstrained region. To constrain the solution, previous works have applied weighted Tikhonov regularization, which adds an additional penalty based on the magnitude of the expansion coefficients as
(13)will attempt to reduce errors at the Q sampling positions with no regard to the expansion in the unconstrained region. To constrain the solution, previous works have applied weighted Tikhonov regularization, which adds an additional penalty based on the magnitude of the expansion coefficients as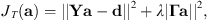 (14)where Γ is a weighting matrix applied to the expansion coefficients a. In the case of unweighted Tikhonov regularization, such as in [18], Γ = I, the identity matrix. The positive scale factor λ determines the strength of the regularization; in the case λ = 0, one obtains the original least-squares solution. The expansion coefficients become (see Eq. (2) of [22])
(14)where Γ is a weighting matrix applied to the expansion coefficients a. In the case of unweighted Tikhonov regularization, such as in [18], Γ = I, the identity matrix. The positive scale factor λ determines the strength of the regularization; in the case λ = 0, one obtains the original least-squares solution. The expansion coefficients become (see Eq. (2) of [22])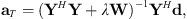 (15)where W = ΓH Γ. This formula gives the least-squares solution (see Eq. (3.34) of [15])
(15)where W = ΓH Γ. This formula gives the least-squares solution (see Eq. (3.34) of [15])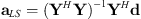 (16)as λ → 0.
(16)as λ → 0.
For sources with documented radiation characteristics, an alternative addition to regularization is to add a penalty term based on the weighted difference between the newly-obtained and previously-known data as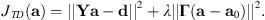 (17)where a0 is the spherical harmonic expansion coefficients of a reference dataset. This form of regularization consequently minimizes errors with respect to differences between measured and expanded values and differences between measured and previously gathered data. This approach has not been applied previously to interpolating voice directivity functions. The expansion coefficients become (see Eq. (2) of [22])
(17)where a0 is the spherical harmonic expansion coefficients of a reference dataset. This form of regularization consequently minimizes errors with respect to differences between measured and expanded values and differences between measured and previously gathered data. This approach has not been applied previously to interpolating voice directivity functions. The expansion coefficients become (see Eq. (2) of [22])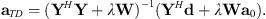 (18)
(18)
In this form of regularization, as λ → 0 one obtains the least-squares solution while as λ → ∞ one obtains aTD = a0. Additional, setting a0 to zero yields the weighted-Tikhonov solution used in previous works; this case represents when no a-priori information is available.
2.4 Comparison of weighting matrices
Even with a given set of measurements d and a reference directivity dataset a0, application of the regularized least-squares fit requires judicious choice of weighting matrix W, the regularization strength λ, and the maximum degree spherical harmonics N. While each of these choices is non-trivial and can lead to different results, previous works have varied on their approaches and implementation of the regularization. This section first clarifies advantages and drawbacks of different weighting matrices.
The weighting matrix W determines how strongly to penalize the magnitude of different terms appearing in a. The unweighted choice (W = I, “white noise” assumption) applied in [18, 21] represents the case where all expansion coefficients should be penalized equally. This assumption is a reasonable choice when little is known about the problem. This weighting is successful at removing the large radiation lobe appearing in the polar gap region compared to the unregularized case [18, 21].
However, knowledge of the physical problem may inform a choice of weighting matrix to improve the result in the unconstrained region. In order to obtain smoother solutions, Aussal et al. [20] instead applied a weighting based on the spherical harmonics’ eigenvalues as (19)with n the degree of the associated spherical harmonic and δij the Kronecker delta. This second-order (∝ n2) penalty strongly discourages the use of coefficients with high n that correspond to large spatial variations. Because the spherical harmonic expansions of sound radiation and scattering exhibit low-pass behavior [18, 23], penalizing higher-degree terms would appear beneficial compared to using an unweighted approach. Nonetheless, Aussal et al. [20] did not provide a direct comparison between the weighted and unweighted results.
(19)with n the degree of the associated spherical harmonic and δij the Kronecker delta. This second-order (∝ n2) penalty strongly discourages the use of coefficients with high n that correspond to large spatial variations. Because the spherical harmonic expansions of sound radiation and scattering exhibit low-pass behavior [18, 23], penalizing higher-degree terms would appear beneficial compared to using an unweighted approach. Nonetheless, Aussal et al. [20] did not provide a direct comparison between the weighted and unweighted results.
To illustrate how each of the weighting matrices influence the final result, Figure 3 plots median plane directivities for the phoneme /a/ in the 1 kHz 1/3rd octave band for three different expansion degrees, N = 4, N = 8, and N = 16. In each case, L-curve analysis after [18] determined the optimal value λ. The talker faces the right towards the 90° marker so that the direction of maximum radiation in this band is in the direction of the talker’s forehead.
 |
Figure 3 Median-plane comparisons between weighting matrices for voice directivity interpolations of the phoneme /a/ at the 1 kHz 1/3rd octave band using N = 4, N = 8, and N = 16 degree expansions. The dotted black line represents phoneme-averaged speech results averaged across six talkers from [12]. |
Several important trends appear. First, across N, the choice of weighting most significantly impacts the expansion in the unconstrained region below the talker’s legs. In the measured region, different weightings yield almost exactly the same interpolated directivity results. However, the results do vary among weightings in the polar gap region. Qualitatively, the unweighted regularization, indicated by solid red lines, shows the most variation in the polar gap region, with a number of spurious radiation lobes appearing which are not present, for example, in the previously published phoneme-averaged spherical results of [12] plotted as thin dotted black lines. Increasing the expansion degree N increases the number of lobes appearing in this region. While the unweighted regularization has ensured that the polar gap region does not become the primary radiation lobe as is the case for the unregularized least-squares results, the number of these smaller radiation lobes suggests that the unweighted regularization is less ideal.
The weighted-regularization, shown as the dashed blue line, successfully suppresses high spatial variations in the unconstrained region. This allows the weighted result to have better agreement with previously published results for all cases of N in the polar gap region. This result emphasizes the strong influence of weighting matrix choice on interpolated results in the polar gap region.
2.5 Hyper-parameter tuning
Besides the weighting matrix W, the regularized least-squares fit requires choice of λ and N. Previous works either used a fixed value [20], ad-hoc determination [21], or L-curve analysis [18] to determine λ. Typically, source geometry determined the choice for the truncation degree N [18, 20]; previous works did not consider the relation between N and λ. However, knowledge of the physical problem suggests at two-step approach to setting λ and N.
It is first beneficial to consider the behavior of the fit based on varying hyper-parameter values. For very small values of λ, the regularized least-squares solution reduces to the unregularized case which fits to the data well at the measurement points (small value of ||Ya – d||2) but may introduce spurious radiation lobes in the unconstrained region below the talker, resulting in a large value of ||Γa||2. As λ increases, the regularization favors expansions using lower rather than higher-order terms (thus decreasing ||Γa||2), which can remove spurious lobes in the unconstrained region.
However, if λ is too high, the solution becomes too biased and the resultant pattern will poorly fit to the measured data points (||Ya – d||2 becomes unacceptably large). Consequently, over increasing λ, one anticipates a valley of stability where optimal fitting results occur, simultaneously obtaining both good agreement between the fit and the measured data as well as the removal of any spurious radiation lobes. L-curve analysis attempts to estimate this valley by computing the curvature of a plot of ||Γa||2 versus ||Ya – d||2 for varying λ [22]. The L-curve estimate represents the point which balances small reconstruction errors with a well-constrained expansion a.
The maximum spherical harmonics degree N determines the spatial complexity of the pattern. Directivity patterns tend to become more complex at higher frequencies, requiring a higher N over increasing frequency [24]. Too few terms means that details in the pattern are smoothed or lost. In contrast, because the expansion coefficient’s behavior is generally low-pass [23], adding additional coefficients above a certain degree does not further benefit the expansion and significantly increases the computational burden in wave-based applications. Consequently, an optimal choice of the hyper-parameters N and λ should (1) provide good agreement between the fitted results and measured data, (2) remove any unphysical radiation lobes in the polar-gap region, and (3) avoid use of an unnecessarily high N.
The relationship between N and λ remains unclear from previous works. The use of weighted regularization, which improves interpolated results in the polar gap region, also penalizes high N. This choice smooths results and may decrease the source order. While L-curve analysis provides a rigorous approach to analyze the bias-variance tradeoff for fixed N, it does not translate to how physically meaningful the results are. For example, the unweighted fit using L-curve optimized λ appearing in Figure 3 had spurious radiation lobes which do not appear in previous spherical results. Proper analysis of optimal values of N and λ consequently requires further validation.
One approach to validate the interpolated results is a comparison with previously published data. Let a0 be the expansion coefficients of a known spherical voice directivity function. Then minimizing an objective function based on a normalized spherical correlation coefficient (see Eq. (1.88) of [15]) as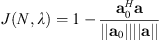 (20)selects the parameters N and λ which minimize the differences between the known directivity a0 and the interpolated directivity represented by a. Note that this definition normalizes J so that when a0 ∝ a, J = 0 while when a0 ⊥ a, J = 1. Because each speech subject and each phoneme may have unique radiation patterns [12], the optimal values of N and λ associated with the minimum of J do not necessarily correspond to optimal fitting parameters of the measured subject. Nonetheless, this approach provides complimentary insights into optimal choices of N and λ compared to L-curve analysis alone.
(20)selects the parameters N and λ which minimize the differences between the known directivity a0 and the interpolated directivity represented by a. Note that this definition normalizes J so that when a0 ∝ a, J = 0 while when a0 ⊥ a, J = 1. Because each speech subject and each phoneme may have unique radiation patterns [12], the optimal values of N and λ associated with the minimum of J do not necessarily correspond to optimal fitting parameters of the measured subject. Nonetheless, this approach provides complimentary insights into optimal choices of N and λ compared to L-curve analysis alone.
To illustrate the features of this objective function, Figure 4a plots the objective function surface over the hyper-parameter space for the case of unweighted regularization (W = I). The reference data consists of phoneme-averaged results averaged across three male and three female talkers taken from [12]. The red squares appearing over the objective function surface mark optimal values of λ given N through L-curve analysis. For values of N approximately greater than 5, the anticipated valley of stability appears, with correlation deviations being less than −20 dB. The L-curve optimal points fall into this valley, and stabilize near a value of λ ≈ 0.5 above N = 10.
 |
Figure 4 Objective function [20log10(J)] plotted over the hyper-parameter space for the vowel /a/ in the 1 kHz 1/3rd octave band using the (a) unweighted and (b) weighted regularization. |
However, the optimal (N, λ) pair selected by L-curve analysis does not always correspond to the lowest possible deviations between the reference directivity. For example, an expansion at N = 7, λ = 0.01 gives a correlation deviation of less than −30 dB. Nonetheless, the L-curve results do roughly correspond to regions of reduced deviations between the reference data.
Using the weighted regularized fit yields a slightly different objective function surface. Figure 4b shows results using the weighted Tikhonov regularization. Again, for values of N approximately greater than 5, the anticipated valley of stability appears. However, the correlation deviations are lower than for the unweighted case, reaching levels below −40 dB. The region corresponds to values of λ ≈ 5. The width of this narrow region with respect to λ appears independent of N as long as N is sufficiently high (N 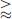 5).
5).
The L-curve points fall slightly below the region of lowest deviations. Above N = 3, they consistently fall at a value of approximately λ ≈ 0.5. Thus, with both weightings, the L-curve analysis and objective functions suggest that λ may be chosen independent of N for a given frequency. This behavior seen in J and the L-curve results suggests a two-step approach to identify optimal values of λ and N. First, determine an optimal value for λ based on a high-degree expansion of the results. Then, using the fixed value of λ, increase N until obtaining desired convergence. This is in contrast to previous works, which used source geometry-based formulas to estimate N and then attempted to find an optimal value for λ.
Figure 5 demonstrates convergence over N for fixed λ for the case of the vowel /a/ at the 1.6 kHz 1/3rd octave band. For a fixed value of λ = 0.5, a directivity factor function deviation level LQ [25]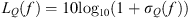 (21)where
(21)where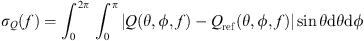 (22)and the directivity factor function is defined as [24]
(22)and the directivity factor function is defined as [24]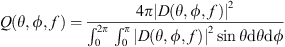 (23)monitors the convergence over increasing N. An N = 35 degree expansion serves as the reference directivity factor function Qref.
(23)monitors the convergence over increasing N. An N = 35 degree expansion serves as the reference directivity factor function Qref.
 |
Figure 5 (a) Directivity deviation levels LQ of directivities producing with increasing maximum expansion degree N relative to an expansion incorporating an N = 35 degree expansion. Directivity balloons expanded using up to (b) N = 3, (c) N = 6, (d) N = 10, and (e) N = 15 degree expansion. In all cases, the regularization parameter λ = 0.5. |
Beginning at a value of LQ ≈ 2.9 dB for an N = 0 expansion, the deviation rapidly decreases to below LQ = 0.5 dB by an N = 5 expansion. After this point, the expansion converges more slowly, obtaining values of less than LQ = 0.25 dB by an N = 12 expansion. This elbow point suggests that an N = 5 expansion captures most of the primary directional features when using the weighted regularization at this frequency. Of course, choosing a weighting matrix which penalizes higher-order terms limits the amount of spatial detail possible and possibly lowers the maximum N necessary compared to the unweighted case.
The four directivity balloons appearing in Figure 5b–5e illustrate these differences over increasing expansion degree N. The N = 3 (Fig. 5b) expansion has the same direction of maximum radiation as the higher-degree expansions but does include secondary radiation lobes corresponding to the regions to the talker’s sides. By the N = 6 expansion (Fig. 5c), only minor differences appear between the other higher-degree expansions. Although the N = 10 and N = 15 expansions afford slightly more details, the changes are difficult to observe without careful inspection.
2.6 Impact of reference dataset
The quality of interpolation largely depends on the underlying assumptions made. For example, when interpolating data over the polar gap region, enforcing an assumption of smoothly varying data by applying a weighting matrix significantly decreased deviations compared to the unweighted case as seen in Figure 3. Another tool not considered in previous works for improving the interpolation results in the polar gap region is to apply a reference dataset using equation (18).
Figure 6 plots interpolated results for the phoneme /a/ at the 400 Hz 1/3rd octave band using a weighted Tikhonov regularization, an N = 15 expansion, and λ = 1. At this frequency, a small diffraction lobe appears below the seated talker’s body in the spherical reference dataset (Fig. 6c and dotted blue line in Fig. 6d). However, because the measurements excluded this region, the regularized interpolation without applying previous data simply provides a smooth interpolation below the talker (Fig. 6a and solid red line in Fig. 6d).
 |
Figure 6 Directivity results for the phoneme /a/ at the 400 Hz 1/3rd octave band using N = 15, λ = 1 and regularizing with (a) no reference dataset (b) reference dataset from [12]. (c) Reference dataset from [12]. (d) Median plane polar results. |
When the regularization uses the reference dataset (Fig. 6b) and dashed green line in Figure 6d, two important trends appear. First, in the measured region, both regularized results almost exactly agree, with less than 0.5 dB deviations between their median plane polar plots. However, in the polar gap region, the regularized interpolation using the reference dataset follows the beam pattern of the reference dataset. Thus, this form of regularization allows one to “blend” both newly and previously measured results, using the new information when available and relying on previous data when information is unavailable. Clearly, the results of this form of interpolation will largely depend on the reliability of the reference dataset used. This approach is beneficial in the present work because directional data below the talker is unavailable; the technique may be less useful in the case of a full-spherical measurement.
3 Results
This section presents select spherically interpolated, phoneme-dependent voice directivities. In all cases, N = 15, λ = 1, and a0 is the phoneme-averaged results from [12]. Figure 7 presents select directivity results for the phonemes /a/, /i/, /o/, /m/, and /n/ for the 160 Hz, 315 Hz, 500 Hz, and 1 kHz 1/3rd octave bands. At 160 Hz, the sound radiation is nearly identical across all phonemes and is quasi-omnidirectional. Radiation patterns at 315 Hz begin to show very slight differences between phonemes, such as between /a/ and /n/. Nonetheless, they all share similar features such as the maximum direction of radiation falling slightly below the talker’s mouth, and secondary lobe appearing directly above the talker, and some reduced levels of radiation behind the talker.
 |
Figure 7 1\3rd-octave-band directivities for the phonemes /a/, /i/, /o/, /m/, and /n/ for the 160 Hz, 315 Hz, 630 Hz, and 1 kHz bands. |
At 630 Hz, more distinct differences between phonemes appear. In general the differences are most distinct in the region in front of and above the talker’s head. For example, both /i/ and /n/ show reduced levels at ϑ = 45° whereas /m/ shows strong radiation in this direction. The phonemes /a/ and /o/ appear more similar, although some minor differences appear. More significant differences across phonemes in this band are consistent with the polar plane results in [10, 11].
At 1 kHz, the primary direction of radiation has moved to the direction above the talker’s head. Previous studies on voice radiation, including [12, 26] have also shown this trend. Similar to the 630 Hz band, the phonemes /a/ and /o/ appear most similar, while, /i/, /m/, and /n/ likewise show some similarities. Unlike at 630 Hz, the differences between /m/ and /n/ are not as distinct.
Differences between phonemes continue to arise at higher frequencies (Fig. 8). At 1.25 kHz, /a/ and /i/ have the maximum direction of radiation oriented at the highest angle. In contrast, /o/, and especially /m/ and /n/ have the principal radiation lobe slightly lowered. In all cases, the radiation is slightly above the mouth axis with secondary lobes appearing on the side. At 1.6 kHz, /a/ and /i/ show similar radiation patterns, although the size of the side lobe is less apparent for /i/ than for /a/. The phonemes /o/, /m/, and /n/ are less directional and appear to have stronger radiation from the sides. At 2 kHz, all phonemes appear to have at least two lobes, one slightly above the mouth axis and one slightly below. The effect is most pronounced for the phoneme /o/, although strongly visible in /i/ and /m/ as well. Multiple lobes above 1 kHz also appear also in the results of [12, 25].
 |
Figure 8 1\3rd-octave-band directivities for the phonemes /a/, /i/, /o/, /m/, and /n/ for the 1.25 kHz, 1.6 kHz, 2 Hz, and 2.5 kHz bands. |
By 2.5 kHz the radiation appears directed forward, although /a/ appears more similar to the radiation pattern of /o/ at 2 kHz. The phoneme /i/ has a narrower beam, while /o/, /m/, and /n/ have wider lobes. These few select results show that while the radiation patterns of many phonemes appear similar, distinct differences arise, particularly in the region 630 Hz to 2 kHz. These same trends were observed in polar-plane results appearing in [10].
4 Analysis
4.1 Signal-to-noise ratio
Different phonemes produce different amounts of energy in different frequency bands. Consequently, determining meaningful phoneme-dependent directivities requires careful analysis of SNR to ensure adequate radiated energy. Figure 9 plots the SNR for three vowels /a/, /i/, /o/, and three consonants /f/, /t∫/, /n/ over the range of 80 Hz to 10 kHz. For these voiced phonemes (the three vowels and /n/), the highest SNR ratio of around 30 dB occurs at the talker’s fundamental frequency near 100 Hz. The SNR levels follow the tonal nature of voiced sounds, being highest at integer multiples of the fundamental and lowest in between partials, where there is little radiated sound. For these four phonemes, the SNR levels slowly decrease to around 15 dB by 3 kHz, after which they rapidly drop off above 4 kHz to around −10 dB.
 |
Figure 9 Signal-to-noise ratios over frequency for three vowels and three consonants. |
The unvoiced phonemes show markedly different trends than the voiced ones. Overall, their SNR levels are lower than for the voiced phonemes, with the SNR levels more evenly distributed over frequency. The softer phoneme /f/ has its highest SNR levels of around 6 dB in the range of 300 Hz to 800 Hz, whereas the phoneme /t∫/ has its highest SNR levels of around 15 dB from 2 kHz to 4 kHz. For all phonemes, the SNR closely reflected the levels of the averaged input autospectrum Gxx,ave(f). These results highlight that confidence in the produced voice directivity patterns varies over frequency and over phoneme, as different phonemes produce energy over different bands.
4.2 Repeatability
Considering the repeatability of subjects when using a repeated rotating array protocol is essential as subjects cannot exactly repeat the same excitation for each repeated capture. The proposed method is grounded in approximating voice radiation as a linear, time-invariant system for the same utterance. While typical sound pressure levels produced during normal speech do not merit consideration of non-linear acoustic propagation effects, the time-varying features of the moving mouth are more problematic. For each utterance, the subject may not exactly reproduce the same mouth shape for a given phoneme, which could alter levels, spectral composition, and even directivity patterns.
During the measurement sequence, the subjects repeated some of the phonemes twice, meaning that comparisons between spherical directivities produced from each of the two repetitions provides a means to assess measurement variance. Figure 10 plots LQ values over frequency between the two repetitions for six different phonemes, /a/,/i/,/o/, /f/, /t∫/ and /m/, based on the spherically interpolated results. For the voiced phonemes, deviations between the two repetitions remained below 0.5 dB up to 500 Hz. Above 500 Hz, the deviations begin to increase, although none exceed 1 dB by 4 kHz. Additionally, all voiced phonemes except /a/ remained below 1 dB up to at least 10 kHz. The frequency-averaged value from 100 Hz to 10 kHz was 0.4 dB, 0.3 dB, 0.3 dB, and 0.3 dB for /a/, /i/, /o/, and /m/, respectively.
 |
Figure 10 Directivity factor deviation level LQ between directivities produced from two repetitions of the same phoneme. |
The unvoiced phonemes /f/ and /∫/ had lower repeatability compared to the voiced phonemes, with frequency-averaged values of 0.6 dB and 0.6 dB, respectively. As suggested by the SNR plots, these phonemes radiated less signal energy and thus had lower coherence values. Regions of lower SNR correspond well with regions of higher deviations between the two repeated takes. This trend highlights the important relationship between radiated levels, coherence, and repeatability of directivity results, whether they reply to measurement protocols using single or multiple captures.
While it may seem surprising that deviations remained low, one should remember that the size of an acoustic wavelength relative to geometrical uncertainties is very small for frequencies of interest. For example, even at 10 kHz, the associated 3.4 cm wavelength is just approaching the size of the entire mouth. Geometric differences in mouth shape between repeated utterances of the same phoneme should be on the order of a few millimeters. Consequently, one cannot anticipate dramatic changes in directivity patterns due to slight variations in mouth size when producing the same phoneme. Of course, these variations may be more significant when considering the effects of co-articulation or for varying levels of loudness, which is beyond the scope of the present work.
Another factor influencing the low deviation levels is the use of the weighted regularization to produce the spherical results. This regularization strongly penalizes higher-order terms, which in effect smooths directivities. Consequently, the regularization likely removes smaller spatial variations and finer radiation details, leading to lower deviations compared to those that would be produced by directly comparing levels at the measurement positions.
4.3 Comparison with previous work
Another important validation of directivity data is comparisons with previously published results. Figure 11 plots values of LQ over frequency between each phoneme’s directivity and that of the time-averaged results of [12]. Below 500 Hz, deviations between phonemes and the time-averaged speech remain less than 1 dB for the voiced phonemes. For the phonemes /i/ and /m/, the deviations quickly rise at the 630 Hz band, although for /a/ and /o/ the deviations remain less than 1.5 dB. This result is interesting because in Figure 7, /i/ and /m/ have strong differences between those of /a/ and /o/ in the 630 Hz band.
 |
Figure 11 Directivity factor deviation level LQ between directivities of each phoneme and time-averaged results from [12]. |
Above 1 kHz, the deviations steadily rise for all phonemes, although none increase beyond 3 dB. The frequency-averaged results were 1.1 dB, 1.3 dB, 1.1 dB, and 1.6 dB, for /a/, /i/, /o/, and /m/, and 1.3 dB and 1.6 dB for /f/ and /t/, respectively. However, because the interpolations incorporated the reference set, these levels are slightly biased; frequency-averaged values when not using the reference set in the interpolation increased the deviation levels by roughly 0.1–0.2 dB. Thus, while differences between exist between individual phonemes, particularly above 500 Hz, the results remained similar to phoneme-averaged values.
5 Conclusions
This work reported on a method for interpolating directivity data measured on two interleaved measurements over the sphere using a regularized least-squares approach. It determined than in interpolated voice directivities, the weighted Tikhonov regularization performed better than the unweighted Tikhonov regularization in the polar gap region. Incorporation of reference data into the regularization likewise improved interpolated results in this region. The work proposed a two-step method to determine the amount of regularization and maximum spherical harmonic degree by comparing fitted results to previously published data. Future works includes detailed correlation and clustering analysis between the directivities of distinct phonemes. Additional work will also analyze the perceptual relevance of incorporating phoneme-dependent directivities in virtual acoustics simulations.
Funding
This work was carried out in part in the context of the SONICOM project (https://www.sonicom.eu) that has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 101017743.
Conflict of interest
The authors declare no conflict of interests.
Data availability statement
Data are available from the authors upon reasonable request.
References
- T. Halkosaari, M. Vaalgamaa, M. Karjalainen: Directivity of artificial and human speech. Journal of the Audio Engineering Society 53 (2005) 620–631. [Google Scholar]
- D. Cabrera, P.J. Davis, A. Connolly: Long-term horizontal vocal directivity of opera singers: effects of singing projection and acoustic environment. Journal of Voice 25 (2011) 291–303. [Google Scholar]
- AES56-2008 (r2019): AES standard on acoustics – Sound source modeling – Loudspeaker polar radiation measurements, Audio Engineering Society, New York, NY, 2019. [Google Scholar]
- CLF Group: CLF: A common loudspeaker format. Syn-Aud-Con News 32 (2004) 14–17. [Google Scholar]
- Ahnert Feistel Media Group: GLL: A new standard for measuring and storing loudspeaker performance data, 2007. Availabale at https://www.afmg.eu/en/gll-loudspeaker-data-format-white-paper. [Google Scholar]
- H.K. Dunn, D.W. Farnsworth: Exploration of pressure field around the human head during speech. Journal of the Acoustical Society of America 10 (1939) 184–199. [CrossRef] [Google Scholar]
- A. Moreno, J. Pretzschner: Human head directivity in speech emission: a new approach. Acoustics Letters 1 (1978) 78–84. [Google Scholar]
- W.T. Chu, A.C. Warnock: Detailed directivity of sound fields around the human head during speech. Research Report IRC-RR-104. National Research Council Canada, 2002. [Google Scholar]
- F. Bozzoli, M. Viktorovitch, A. Farina: Balloons of directivity of real and artificial mouth used in determining speech transmission index, in: Proceedings of the 118th Audio Engineering Society Convention, Barcelona, Spain, May 28–31 2005, 2005, pp. 1–5. Paper 6492. [Google Scholar]
- B.F.G. Katz, F. Prezat, C. d’Alessandro: Human voice phoneme directivity pattern measurements. Journal of the Acoustical Society of America 120 (2006) 3359–3359. [CrossRef] [Google Scholar]
- B.F.G. Katz, C. D’Alessandro: Directivity measurements of the singing voice, in: Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September, 2007. [Google Scholar]
- T.W. Leishman, S.D. Bellows, C.M. Pincock, J.K. Whiting: High-resolution spherical directivity of live speech from a multiple-capture transfer function method. Journal of the Acoustical Society of America 149 (2021) 1507–1523. [CrossRef] [PubMed] [Google Scholar]
- C. Pörschmann, J.M. Arend: A method for spatial upsampling of voice directivity by directional equalization. Journal of the Audio Engineering Society 68 (2020) 649–663. [CrossRef] [Google Scholar]
- C. Pörschmann, J.M. Arend: Investigating phoneme-dependencies of spherical voice directivity patterns. The Journal of the Acoustical Society of America 149 (2021) 4553–4564. [CrossRef] [PubMed] [Google Scholar]
- B. Rafaely: Fundamentals of spherical array processing. Springer-Verlag, Berlin Heidelberg, 2015. [CrossRef] [Google Scholar]
- L. Savioja, U.P. Svensson: Overview of geometrical room acoustic modeling techniques. Journal of the Acoustical Society of America 138 (2015) 708–730. [Google Scholar]
- S.D. Bellows, T.W. Leishman: Optimal microphone placement for single-channel sound-power spectrum estimation and reverberation effects. Journal of the Audio Engineering Society 71 (2023) 20–33. [CrossRef] [Google Scholar]
- D. Zotkin, R. Duraiswami, N. Gumerov'‘ Regularized HRTF fitting using spherical harmonics, in: IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, 18–21 October, 2009, IEEE, pp. 257–260. [Google Scholar]
- P.C. Hansen: Regularization tools: A MATLAB package for analysis and solution of discrete ill-posed problems. Numerical Algorithms 6 (1994) 1–35. [CrossRef] [Google Scholar]
- M. Aussal, F. Alouges, B. Katz: A study of spherical harmonics interpolation for HRTF exchange. Proceedings on Meetings in Acoustics 19 (2013) 1–9. [Google Scholar]
- S.D. Bellows, T.W. Leishman: Obtaining far-field spherical directivities of guitar amplifiers from arbitrarily shaped arrays using the Helmholtz equation least-squares method. Proceedings of Meetings on Acoustics 42 (2020) 055005. [CrossRef] [Google Scholar]
- P.C. Hansen, The L-curve and its use in the numerical treatment of inverse problems, in: P. Johnston (Ed.), Computational inverse problems in electrocardiology, WIT Press, 2001, pp. 119–142. [Google Scholar]
- S.D. Bellows, T.W. Leishman: A spherical-harmonic-based framework for spatial sampling considerations of musical instrument and voice directivity measurements, in: 10th Convention of the European Acoustics Association, Turin, Italy, 11th–15th September 2023. [Google Scholar]
- L. Beranek, T. Mellow: Acoustics: Sound fields, transducers and vibration, 2nd edn., Academic Press, 2019. [Google Scholar]
- S. Bellows, T.W. Leishman: Effect of head orientation on speech directivity, in: Procceedings of 23rd Interspeech, Incheon, South Korea, September 18–22, 2022, pp. 246–250. [Google Scholar]
- M. Brandner, R. Blandin, M. Frank, A. Sontacchi: A pilot study on the influence of mouth configuration and torso on singing voice directivity. Journal of the Acoustical Society of America 148 (2020) 1169–1180. [CrossRef] [PubMed] [Google Scholar]
Cite this article as: Bellows SD. & Katz BFZ. 2024. Combining multiple sparse measurements with reference data regularization to create spherical directivities applied to voice data. Acta Acustica, 8, 14.
All Figures
 |
Figure 1 Directivity measurement system including the rotating arc, reference microphone and rotating chair. |
| In the text | |
 |
Figure 2 Sampling positions produced from the front, side, and reflected side configurations. |
| In the text | |
 |
Figure 3 Median-plane comparisons between weighting matrices for voice directivity interpolations of the phoneme /a/ at the 1 kHz 1/3rd octave band using N = 4, N = 8, and N = 16 degree expansions. The dotted black line represents phoneme-averaged speech results averaged across six talkers from [12]. |
| In the text | |
 |
Figure 4 Objective function [20log10(J)] plotted over the hyper-parameter space for the vowel /a/ in the 1 kHz 1/3rd octave band using the (a) unweighted and (b) weighted regularization. |
| In the text | |
 |
Figure 5 (a) Directivity deviation levels LQ of directivities producing with increasing maximum expansion degree N relative to an expansion incorporating an N = 35 degree expansion. Directivity balloons expanded using up to (b) N = 3, (c) N = 6, (d) N = 10, and (e) N = 15 degree expansion. In all cases, the regularization parameter λ = 0.5. |
| In the text | |
 |
Figure 6 Directivity results for the phoneme /a/ at the 400 Hz 1/3rd octave band using N = 15, λ = 1 and regularizing with (a) no reference dataset (b) reference dataset from [12]. (c) Reference dataset from [12]. (d) Median plane polar results. |
| In the text | |
 |
Figure 7 1\3rd-octave-band directivities for the phonemes /a/, /i/, /o/, /m/, and /n/ for the 160 Hz, 315 Hz, 630 Hz, and 1 kHz bands. |
| In the text | |
 |
Figure 8 1\3rd-octave-band directivities for the phonemes /a/, /i/, /o/, /m/, and /n/ for the 1.25 kHz, 1.6 kHz, 2 Hz, and 2.5 kHz bands. |
| In the text | |
 |
Figure 9 Signal-to-noise ratios over frequency for three vowels and three consonants. |
| In the text | |
 |
Figure 10 Directivity factor deviation level LQ between directivities produced from two repetitions of the same phoneme. |
| In the text | |
 |
Figure 11 Directivity factor deviation level LQ between directivities of each phoneme and time-averaged results from [12]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


