| Issue |
Acta Acust.
Volume 4, Number 1, 2020
|
|
|---|---|---|
| Article Number | 1 | |
| Number of page(s) | 17 | |
| Section | Audio Signal Processing and Transducers | |
| DOI | https://doi.org/10.1051/aacus/2019001 | |
| Published online | 28 February 2020 | |
Original Article
Passive modelling of the electrodynamic loudspeaker: from the Thiele–Small model to nonlinear port-Hamiltonian systems
1
M2N Team, Laboratory LaSIE (UMR 7356), CNRS, Université de La Rochelle, 17042
La Rochelle Cedex 1, France
2
CNRS, S3AM Team, Laboratory STMS (UMR 9912), IRCAM-CNRS-SU, 1 Place Igor Stravinsky, 75004
Paris, France
* Corresponding author: antoine.falaize@univ-lr.fr
The electrodynamic loudspeaker couples mechanical, magnetic, electric and thermodynamic phenomena. The Thiele/Small (TS) model provides a low frequency approximation, combining passive linear (multiphysical or electric-equivalent) components. This is commonly used by manufacturers as a reference to specify basic parameters and characteristic transfer functions. This paper presents more refined nonlinear models of electric, magnetic and mechanical phenomena, for which fundamental properties such as passivity and causality are guaranteed. More precisely, multiphysical models of the driver are formulated in the core class of port-Hamiltonian systems (PHS), which satisfies a power balance decomposed into conservative, dissipative and source parts. First, the TS model is reformulated as a linear PHS. Then, refinements are introduced, step-by-step, benefiting from the component-based approach allowed by the PHS formalism. Guaranteed-passive simulations are proposed, based on a numerical scheme that preserves the power balance. Numerical experiments that qualitatively comply with measured behaviors available in the literature are presented throughout the paper.
© A. Falaize and T. Hélie, Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The electrodynamic loudspeaker is a non ideal transducer. Its dynamics is governed by intricate multiphysical phenomena (mechanical, magnetic, electric and thermodynamic), a part of which involves nonlinearities responsible for audio distortions [1–3]. As a first example, the viscoelastic properties of the suspension material result in long-term memory (linear) and hardening spring effect (nonlinear). Second, the ferromagnetic properties of the solid iron core in the voice-coil result in eddy current losses (linear) and magnetic saturation (nonlinear). Third, the resistance of the coil wire converts a part of electrical power into heat. This modifies material properties and, eventually, can cause irreversible damages. Such phenomena must be modeled and considered in the design of real-time distortion compensation [4–7] and that of burn-out protection [2, 8].
The basic reference set of parameters describing the electrodynamic loudspeaker is that of Thiele–Small [9–12]. In the sequel, we refer to this set of parameters as the Thiele–Small model. It combines passive linear models of elementary physical components (see Fig. 1) and provides a low-frequency linear time-invariant approximation for low-amplitude excitation on short period. This (multiphysical or electric-equivalent) parametric model is commonly used by manufacturers as a reference to specify basic parameters and characteristic transfer functions.
 |
Figure 1 Schematic of the electrodynamic loudspeaker and components labels. |
Various refinements of this reference model have been proposed, both in the frequency domain and the time domain [3, 13–18]. In particular, the lumped-parameter approach [1, 2, 19, 20] consists in modeling the dependence of Thiele–Small parameters on some selected physical quantities (e.g. position-dependent stiffness). However, fundamental physical properties are usually not guaranteed by the proposed mathematical models, and their physical interpretation is not always obvious. Examples are model causality in the context of frequency domain simulation based on Fourier transform and model passivity in the context of arbitrary polynomial approximation of constitutive relations of materials. Obviously, this is also the case for gray-box modelling based on Volterra and Wiener/Volterra series [21–24] or nonlinear ARMAX [25]).
To circumvent those difficulties, we introduce the port-Hamiltonian systems formalism [26–28] as a systematic framework for the nonlinear modeling, simulation and control of loudspeakers. Port-Hamiltonian systems are state-space representations that satisfy a power balance structured into conservative, dissipative and external(/source) parts. This structure can be described by acausal graphs (such as electronic circuits or classical electromechanical analogies) which allow modular exploration or local model refinements, while guarantying passivity. Such modular processes are facilitated by existing methods [29] that automatically generate the governing equations associated with a given multiphysical system described by a network of predefined or user-defined components. It is then possible to run guaranteed-passive simulations based on a numerical method that preserves the power balance and its structure in the discrete-time domain, from which passivity and stability properties stem. The objective of this work is to model well-known multiphysical phenomena occurring in loudspeakers as a set of port-Hamiltonian structures and components in view of system identification and correction.
The elementary phenomena that are considered in this paper are concerned with mechanical, magnetic and electric phenomena, as well as their coupling. They are known to be responsible for significant audio distortions (see e.g. [1, 2] and references therein):
-
The materials used for the suspension (S) exhibit, first, a combination of the behaviors of elastic solids and viscous fluids ([30], Sect. 1.2), inducing long time shape memory (creep effect, see e.g. Fig. 1 from [30] and Fig. 11 from [31]) and second, nonlinear stress–strain characteristics so that the restoring force is not proportional to the elongation [1, 18], with maximal instantaneous excursion qsat that corresponds to the breakdown of the material.
-
The electromechanical coupling (back e.m.f. and Lorentz force on the diaphragm D) depends on the coil (C) position and on the magnetic flux in the pole piece (P). The former is modulated by the movement of the coil which acts as an electromagnet that modifies the latter.
-
The materials used for the pole piece P exhibit nonlinear magnetic excitation–induction curve so that the equivalent current in the coil is not proportional to its magnetic flux. Also, a maximal magnetic flux ϕsat is reached (flux saturation), corresponding to the global alignment of the microscopic magnetic moments (see [32] Sect. 1 and Ref. [33]).
-
Most of the magnetic materials (iron, cobalt, etc.) possess high electric conductivity. The application of a variable magnetic induction induces currents, namely eddy-currents, in a plane orthogonal to the field lines (see [34], Sect. 1.1.2). This has three effects: a power is dissipated due to the natural resistivity of the material (Joule effect), eddy-currents induces their own magnetic field (added inductive effect), and they oppose to the original induction (Lens’s law), which pushes the field lines toward the boundary (magnetic skin effect).
This paper is structured as follows. Section 2 recalls the Thiele–Small model (model 0) which recast as a port-Hamiltonian system after a short introduction to the formalism. This model 0 serves as a basis to elaborate two refined loudspeaker models (model 1 and model 2). Section 3 focuses on refinements of the mechanical part (model 1). In particular, a passive-guaranteed nonlinear model based on the Kelvin–Voigt description of viscoelastic material associated with the suspension (S) is provided. Section 4 focuses on refinements of the electromagnetic part (model 2). In particular, we provide a lumped parameter non linear description of the full magnetic circuit (M, P) coupled with the electronic circuit and the mechanical system. These passive models can straightforwardly be combined to describe all these refinements in a single model. Simulations are presented throughout the paper, focusing on the effect of each phenomena, separately. In practice, they are all1 produced by the PyPHS software [35].
2 The Thiele–Small model revisited in the port-Hamiltonian formalism
This section is devoted to the construction of the base model (model 0) that is progressively refined in the remaining of the paper. First, an overview of the functioning of the electrodynamic loudspeaker is presented and the standard Thiele–Small modeling is recalled. Second, the port-Hamiltonian framework is recalled. Third, the Thiele–Small model is recast as a port-Hamiltonian system (model 0). Finally, time-domain simulations are performed and results are compared in the frequency-domain to transfer functions expected from filter theory.
2.1 Standard Thiele/Small model
The basic functioning of a boxed loudspeaker such as the one depicted in Figure 1 is as follows. A voice-coil (C) submitted to an input voltage (I) is immersed in a magnetic field imposed by a permanent magnet (M) in the air gap (G) of a magnetic path (pole piece P), so that the coil (C) is subjected to the Lorentz force. The coil (C) is glued to a large diaphragm (D) which is maintained by a flexible suspension (S). The diaphragm (D) is responsible for the coupling with the acoustical field (A).
The standard description of the dynamics of this system is referred as the Thiele–Small modeling, introduced in the early seventies [9–12]. The electrical part (C) includes the electrical resistance of the coil wire RC and the linear approximation of the coil behavior with inductance LC. The mechanical part (C, D, S, A) is modeled as a damped harmonic oscillator with mass MCDA (coil, diaphragm and additional mass due to acoustic radiation), linear approximation of the spring effect KSA (suspension and additional stiffness due to air compression in the enclosure) and fluid-like damping with coefficient RSA (frictions and acoustic power radiation). The magnetic part (M, P, G, C) reduces to a constant force factor  .
.
The corresponding set of ordinary differential equations are derived by applying Kirchhoff’s laws to the electrical part (C) and Newton’s second law to the mechanical part (D, S, A):
 (2)with vI the input voltage, iC the coil current and qD the diaphragm’s displacement from equilibrium. The electromechanical coupling terms are the back electromotive force (voltage)
(2)with vI the input voltage, iC the coil current and qD the diaphragm’s displacement from equilibrium. The electromechanical coupling terms are the back electromotive force (voltage)  and the Lorentz force
and the Lorentz force  .
.
2.2 Port-Hamiltonian formalism
The port-Hamiltonian (pH) formalism introduced in the 90’s [26] is a modular framework for the passive-guaranteed modeling of open dynamical systems. In this paper, we consider the following class formulated as a multiphysical, component-based, differential algebraic state-space representation (as in [29]).
Definition 2.1
(Port-Hamiltonian Systems, PHS). The class of PHS under consideration is that of differential algebraic state-space representations with input
 , state
, state
 , output
, output
 , that are structured according to energy flows and described by (see [29] for details and [26–28] for more general formulations of PHS):
, that are structured according to energy flows and described by (see [29] for details and [26–28] for more general formulations of PHS):
 (3)
where
(3)
where
 stands for dissipation variables with dissipation law
stands for dissipation variables with dissipation law
 ,
,
 is the energy storage function (or Hamiltonian) with gradient
is the energy storage function (or Hamiltonian) with gradient
 ,
,
 ,
,
 ,
,
 , and where
, and where
the storage function H(x) is positive semidefinite H(x) ≥ 0 with H(0) = 0 and positive definite Hessian matrix
![$ [{\mathcal{H}}_{\mathrm{H}}(\mathbf{x}){]}_{i,j}=\frac{{\mathrm{\partial }}^2\mathrm{H}}{\mathrm{\partial }{x}_i,\mathrm{\partial }{x}_j}(\mathbf{x})$](/articles/aacus/full_html/2020/01/aacus190001s/aacus190001s-eq17.gif) (see examples inAppendix C),
(see examples inAppendix C),the dissipation lawz(w) is null at originz(0) = 0 with positive definite Jacobian matrix
![$ [{\mathcal{J}}_{\mathbf{z}}(\mathbf{w}){]}_{i,j}=\frac{\mathrm{\partial }{z}_i}{\mathrm{\partial }{w}_j}(\mathbf{w})$](/articles/aacus/full_html/2020/01/aacus190001s/aacus190001s-eq18.gif) , implying that the dissipated power is PD (w) = z(w)Tw ≥ 0, PD (0) = 0,
, implying that the dissipated power is PD (w) = z(w)Tw ≥ 0, PD (0) = 0,
 ,
,
 and
and  are skew-symmetric matrices, so thatJT = −J.
are skew-symmetric matrices, so thatJT = −J.
System (3) proves passive for the outgoing power PS = u T y according to the following power balance:
 (4)This proves the passivity and hence the asymptotic stability of (3) in the sense of Lyapunov ([36], Sect. 4).
(4)This proves the passivity and hence the asymptotic stability of (3) in the sense of Lyapunov ([36], Sect. 4).
Remark 2.2
(Energy storage) The Hamiltonian considered in this work does not depend explicitly on time so that it coincides with the total energy in the system:

2.3 The Thiele–Small model as a PHS
The Thiele–Small modeling from Section 2.1 can be regarded as the interconnection of a resistance-inductance circuit with a mass-spring-damper system, through a gyrator that describes the reversible energy transfer from the electrical domain to the mechanical domain as depicted in Figure 2 and detailed in Section B.2.
 |
Figure 2 Equivalent circuit with direct electromechanical analogy (force ↔ voltage, velocity ↔ current) that corresponds to the Thiele–Small model (1) and (2) with electromechanical coupling |
Description
This system includes nx
= 3 storage components (inductance LC, mass MCDA and stiffness KSA), nw
= 2 dissipative components (electrical resistance RC and mechanical damping RSA) and ny
= 1 port (electrical input vI). The state  consists of the magnetic flux in the coil ϕC, mass momentum
consists of the magnetic flux in the coil ϕC, mass momentum  and diaphragm position qD. The Hamiltonian is the sum of the electrodynamic energy
and diaphragm position qD. The Hamiltonian is the sum of the electrodynamic energy  , the kinetic energy
, the kinetic energy  and the potential energy
and the potential energy  . The dissipation variable is
. The dissipation variable is  with linear dissipation law
with linear dissipation law  .
.
Port-Hamiltonian formulation
The above PHS quantities are related with quantities in the Thiele–Small model (1) and (2) as follows:
Electrical part:

Mechanical part:

 and the Lorentz force
and the Lorentz force  . This yields the following port-Hamiltonian reformulation of (1)–(2):
. This yields the following port-Hamiltonian reformulation of (1)–(2):
 (5)with coil velocity
(5)with coil velocity  and current
and current  . The associated port-Hamiltonian structure (3) is given in Table 1.
. The associated port-Hamiltonian structure (3) is given in Table 1.
Simulation results
Simulations are performed following the passive-guaranteed numerical method associated with the pH structure (3) and recalled in Appendix A. Time domain simulations are shown in Figure 3. Transfer function computed from time domain simulation  with s the complex frequency is shown in Figure 4. Notice the (numerical) power balance is satisfied. The model 0 in Table 1 is refined in the sequel to cope with the phenomena listed in the introduction.
with s the complex frequency is shown in Figure 4. Notice the (numerical) power balance is satisfied. The model 0 in Table 1 is refined in the sequel to cope with the phenomena listed in the introduction.
 |
Figure 3 Simulation results for the model 0 in Table 1. Physical parameters are given in Table D1. The input voltage vI is a 100 Hz sine wave with increasing amplitude between 0 and 50 V. The sampling rate is Fs = 96 kHz. |
 |
Figure 4 Transfer functions from the simulation of the model 0 in Table 1 (phs) and computed from filter theory (target). Physical parameters are given in Table D1. The input voltage vI is a 1 V white noise and the sampling rate is Fs = 96 kHz. |
3 Refined mechanics
In this section, the model 0 from Section 2.3 is refined to cope with creep effect and nonlinear stress-strain relation attached to the suspension material (S). First, we detail the modeling of the creep effect based on Kelvin–Voigt model of viscoelastic material [30, 31]. This results in a linear PHS. Second, the hardening suspension effect is included. This results in a nonlinear PHS (model 1). Third, simulation results are shown.
3.1 Suspension creep
The creep effect is a long-term memory effect due to the shape memory of the suspension material (see e.g. Fig. 1 from [30] and Fig. 11 from [31]) and heat relaxation of the fluid in the enclosure (see e.g. [17]).
In this work, we consider the standard Kelvin–Voigt model for viscoelastic materials. The resulting (linear) mechanical subsystem is depicted in Figure 5 and is recast in this subsection as a port-Hamiltonian system (3). Note the procedure given below allows to formulate other creep models (e.g. from the literature given above) as port-Hamiltonian systems.
 |
Figure 5 Small-signal modeling of the mechanical part which includes: the total mass MCDA (diaphragm, coil and additional mass due to acoustic radiation), the fluid-like damper RSA (mechanical friction and small signal approximation for the acoustic power radiation), primary stiffness K0 and Kelvin–Voigt modeling of the creep effect (K1, R1), with diaphragm position qD, primary elongation q0 and creep elongation q1. Parameters are given in Tables D1 and D2. |
 |
Figure 6 Equivalent circuit for model 1 with diaphragm position qD, primary elongation q0 and creep elongation q1. Elements common to model 0 in Figure 2 are shaded. |
3.1.1 Description of the creep model
Viscoelastic materials exhibit combination of elastic solids behaviors and viscous fluid behaviors. Let R be the coefficient of viscosity for a damper (N · s · m−1) and K the modulus of elasticity for a spring element (N · m−1) with characteristic frequency  (Hz) and associated creep time
(Hz) and associated creep time
 (s). Their respective compliance in the Laplace domain are
(s). Their respective compliance in the Laplace domain are  and
and  where
where  is the complex Laplace variable
is the complex Laplace variable  , and where q(s), fK(s) and f
R
(s) are the Laplace transforms of the elongation and the two restoring forces, respectively.
, and where q(s), fK(s) and f
R
(s) are the Laplace transforms of the elongation and the two restoring forces, respectively.
The Kelvin–Voigt modeling of the creep effect is constructed by connecting a linear spring with same stiffness K in parallel with a damper R (see [37] and Sect. 4 from [38]). The elongation is the same for both elements qkv = q and forces sum up fkv = fK + fR. The corresponding compliance is
The modeling of materials that exhibits several relaxation times  is achieved by chaining N Kelvin–Voig elements (see [20, 38, 39] and Fig. 1 from [37]). Each element contributes to the total elongation
is achieved by chaining N Kelvin–Voig elements (see [20, 38, 39] and Fig. 1 from [37]). Each element contributes to the total elongation  , and every elements experience the same force
, and every elements experience the same force  . Here, we consider three elements to restore (i) a primary instantaneous response to a step force with stiffness K0 and (ii) a long time viscoelastic memory with characteristic time
. Here, we consider three elements to restore (i) a primary instantaneous response to a step force with stiffness K0 and (ii) a long time viscoelastic memory with characteristic time  . The compliance of this viscoelastic model is
. The compliance of this viscoelastic model is
The parameters are K0, K1 and τve
 . A possible strategy to tune jointly the
. A possible strategy to tune jointly the  is to introduce a dimensionless parameter
is to introduce a dimensionless parameter  to partition the Thiele–Small stiffness KSA between K0 and K1:
to partition the Thiele–Small stiffness KSA between K0 and K1:
 (8)Note this choice ensure that
(8)Note this choice ensure that  for all 0 < P
K
< 1 (i.e. the combination of K0 and K1 restores the Thiele–Small stiffness KSA if the creep effect is neglected τve = 0).
for all 0 < P
K
< 1 (i.e. the combination of K0 and K1 restores the Thiele–Small stiffness KSA if the creep effect is neglected τve = 0).
3.1.2 Port-Hamiltonian formulation
The creep model (7) corresponds to the parallel connection of (i) a linear spring K0 and (ii) a linear spring K1 serially connected to a dashpot R1 (see Fig. 5). This mechanical subsystem includes n
x
= 3 storage components (mass MCDA, primary stiffness K0, secondary stiffness K1), n
w
= 2 dissipative components (damper RSA, secondary damper R1), and n
y
= 1 port (Lorentz force fL). The state  includes the mass momentum
includes the mass momentum  , and the primary and secondary elongations q0 and q1 (respectively). The Hamiltonian is the sum of (i) the kinetic energy
, and the primary and secondary elongations q0 and q1 (respectively). The Hamiltonian is the sum of (i) the kinetic energy  , and (ii) the primary and secondary potential energies
, and (ii) the primary and secondary potential energies  and
and  (respectively). The dissipation variable is
(respectively). The dissipation variable is  with linear dissipation law
with linear dissipation law  . The input/output are
. The input/output are  and
and  . For these definitions, the interconnection in Figure 5 yields:
. For these definitions, the interconnection in Figure 5 yields:
 (9)This system is recast as a port-Hamiltonian system (3) for the structure in Table 2 and the parameters in Table D2.
(9)This system is recast as a port-Hamiltonian system (3) for the structure in Table 2 and the parameters in Table D2.
3.2 Suspension hardening and model 1
For large displacement, the suspension behaves like an hardening spring (see e.g. [18, 40]). This should occur for instantaneous displacements, so that only the primary stiffness K0 in Table 2 is affected. First, the mechanical subsystem from previous section is changed to cope with this phenomenon. Second, the resulting nonlinear mechanical part is included in loudspeaker model 0 to build the loudspeaker model 1.
3.2.1 Model description
The primary stiffness K0 in Table 2 is modified into a nonlinear spring that exhibits a phenomenological saturation for an instantaneous elongation q0 = ±qsat (symmetric). The associated constitutive law (C1)–(C3) in Appendix C is
It yields the restoring force f0(q0) = K0 cSA(q0) for the initial stiffness K0. It corresponds to the addition of a saturating term that does not contribute around the origin, thus preserving the meaning of parameter K0 (small signal behavior). The associated storage function (C4) and (C5) is
 (11)Note that any storage function suitable to a particular material could be used (such as for example those given in Appendix C), and that the modular structure of the port-Hamiltonian formalism allows to change the storage function without modifying the interconnection matrix.
(11)Note that any storage function suitable to a particular material could be used (such as for example those given in Appendix C), and that the modular structure of the port-Hamiltonian formalism allows to change the storage function without modifying the interconnection matrix.
3.2.2 Port-Hamiltonian system and Model 1
The port-Hamiltonian formulation of the loudspeaker model 1 includes creep effect and hardening suspension. It is obtained by (i) replacing the potential energy  in Table 2 by the nonlinear storage function (11) and (ii) connecting the mechanical port
in Table 2 by the nonlinear storage function (11) and (ii) connecting the mechanical port  to the RL circuit describing the electromagnetic part as in Section 2.3. This results in the structure given in Table 3 with parameters in Tables D1 and D2.
to the RL circuit describing the electromagnetic part as in Section 2.3. This results in the structure given in Table 3 with parameters in Tables D1 and D2.
Port-Hamiltonian formulation (3) for the model 1 depicted in Figure 6. The linear stiffness  is replaced by the Kelvin–Voigt modeling of the creep effect from Section 3.1 in serial connection with the nonlinear spring described in Section 3.2, with diaphragm position
is replaced by the Kelvin–Voigt modeling of the creep effect from Section 3.1 in serial connection with the nonlinear spring described in Section 3.2, with diaphragm position  , momentum
, momentum  , primary elongation
, primary elongation  , and creep elongation
, and creep elongation  . The nonlinear potential energy
. The nonlinear potential energy  is given in (11). Parameters are given in Tables 4 and D1, with
is given in (11). Parameters are given in Tables 4 and D1, with  and
and  .
.
3.3 Simulation results
The numerical method used to simulate the mechanical subsystem (Tab. 2) and the model 1 (Tab. 3) is detailed in Appendix A. The results obtained for physical parameters in Tables D1 and D2 are commented below.
Creep effect
It is expected that the viscoelastic behavior of the suspension material results in a frequency-dependent compliance, i.e. the suspension at low frequencies must appear softer than for the Thiele/Small prediction (see e.g. [17], Fig. 12). Model 1 allows the recovery of this effect as shown in Figure 7. The corresponding long time memory depicted in Figure 8 is in accordance with measurements in e.g. Figure 1 from [30] and Figure 11 from [31].
 |
Figure 7 Simulation of the small-signal modeling of the mechanical subsystem in Table 2: Compliance in the frequency domain (diaphragm displacement in response to the Lorentz force |
 |
Figure 8 Simulation of the small-signal modeling of the mechanical subsystem in Table 2: diaphragm displacement in response to a 10N Lorentz force step between 0s and 2s (time domain). Note that τve = 0 corresponds to the mechanical subsystem as described by the Thiele–Small model (no creep). |
Nonlinear suspension
The hardening effect associated with the nonlinear stress–strain characteristic of the suspension material is clearly visible in Figure 9 where the primary elongation is reduced for higher value of the shape parameter  . This reduces the total displacement qD and momentum
. This reduces the total displacement qD and momentum  , while the creep elongation is almost unchanged.
, while the creep elongation is almost unchanged.
 |
Figure 9 Simulation of the model 1 in Table 3 depicted in Figure 6, for the parameters in Tables D1 and D2 (except |
4 Refined electromagnetic
In this section, the model 0 from Section 2.3 is refined to account for effects of flux modulation, electromagnetic coupling, ferromagnetic saturation and eddy-current losses attached to the electromagnetic part (voice-coil C, magnet M, ferromagnetic path P and air gap G). First, the proposed modeling is described. Second, this model is recast as a port-Hamiltonian system. Third, simulation results are presented.
4.1 Model description
The classical lumped elements modeling of loudspeakers electrical impedance includes the electrical DC resistance of the wire RC serially connected to a non-standard inductive effect, referred as lossy-inductor. The simplest refinement of the Thiele/Small modeling is the so-called LR-2 model, which uses a series inductor connected to a second inductor shunted by a resistor. Several refinements to this model are available in the litterature [16, 41–44].
The modeling of the loudspeakers electrical impedance proposed in this work is depicted in Figure 10. The coil winding acts as an electromagnetic transducer (gyrator) that realizes a coupling between the electrical and the magnetic domains, according to the gyrator-capacitor approach (see Appendix B.3 and Refs. [45, 46]). The electrical domain includes the linear resistance RC of the coil wire (same as Thiele–Small model) and a constant linear inductance associated with the leakage magnetic flux that does not penetrate the pole piece (P). The flux in the magnetic path is common to (i) a nonlinear magnetic capacitor associated with energy storage in air gap (G, linear) and ferromagnetic (P, nonlinear), (ii) a linear magnetic dissipation associated with eddy-currents losses in the path (P) and (iii) a constant source of magnetomotive force associated with the permanent magnet (Ampere model).
 |
Figure 10 Proposed modeling of the electromagnetic circuit, which includes: the coil wire resistance RC, the linear inductance associated with the leakage flux ϕleak, the electromagnetic transduction with nP the number of wire turns around the magnetic path, the magnetic energy storage in the ferromagnetic path described by the nonlinear induction–excitation curve ψPG(ϕPG) from (15), the linear dissipation associated with eddy-currents in the pole piece, and the constant source of magnetomotive force ψM due to the magnet from (17). |
4.1.1 Coil model
Leakage inductance
A single leakage flux ϕleak = Sleak bleak independent of the position qD is assumed for every of the NC wire turns (see Fig. 10a), with Sleak the annular surface between the coil winding and the ferromagnetic core, computed as
 (12)where 0 < αleak < 1 is the fraction of the coil section not occupied by the magnetic core. According to (B1), the linear magnetic capacity of the air path is
(12)where 0 < αleak < 1 is the fraction of the coil section not occupied by the magnetic core. According to (B1), the linear magnetic capacity of the air path is  with AC the height of the coil wire turns, μ0 the magnetic permeability of vacuum and
with AC the height of the coil wire turns, μ0 the magnetic permeability of vacuum and  the magnetic susceptibility of air. From (B6), this corresponds to an electrical inductance with state xleak = NC
ϕleak and storage function
the magnetic susceptibility of air. From (B6), this corresponds to an electrical inductance with state xleak = NC
ϕleak and storage function  , for the inductance
, for the inductance  . We define the characteristic frequency
. We define the characteristic frequency  (Hz).
(Hz).
Electromagnetic coupling modulation
The electromagnetic coupling between the coil (C) and the path (P) depends on the he number nP of wire turns effectively surrounding the pole piece. For small negative excursions qD < 0 every wire turns participate to the coupling (nP ≃ NC) and for large positive excursions the coil leaves the pole piece (nP ≃ 0). We propose a phenomenological sigmoid relation  :
:
 (13)with nP(q−) ≃ 90% NC and nP(q+) ≃ 10% NC (see Fig. 11).
(13)with nP(q−) ≃ 90% NC and nP(q+) ≃ 10% NC (see Fig. 11).
 |
Figure 11 Plot of the position-dependent effective number of wire turns nP(qD) involved in the electromagnetic coupling from (13) with q+ = 5 mm and q− in the legend. |
 |
Figure 12 Equivalent circuit of the model 2 described in Table 4. Elements common to model 0 in Figure 2 are shaded. The coil inductance LC is replaced by the electromagnetic circuit from Figure 10b which includes the leakage inductance Lleak and the magnetic path (pole piece P and air gap G). |
4.1.2 Ferromagnetic saturation
Nonlinear storage
The storage of magnetic energy in the magnetic circuit is spread over the pole piece (P) and the air gap (G). Assuming no leakage flux in the pole piece, those elements are crossed by the same magnetic flux ϕPG (see Fig. 10a and Refs. [45, 46]). The corresponding averaged inductions are
 (14)with SP the average section crossed by the magnetic flux in the pole piece and SG the section of the flux in the air gap (see Fig. 10a). This corresponds to the serial connection of two magnetic capacitors: the first one is associated with the air gap G with linear constitutive law (as for the leakage flux ϕleak); the second one is associated with the pole piece P and cannot be described by a linear magnetic capacity due to the magnetic saturation that occurs in ferromagnetic material (see [32], Sect. 1). Those two serially-connected magnetic capacitors can merge into a single nonlinear capacitor that restores the total magnetomotive force ψPG(ϕPG). In this work, we consider the tangent-like constitutive relation detailed in Appendix C with flux saturation ϕsat = SP
bsat, where bsat depends on the specific magnetic material. From (C1) to (C3), the constitutive law ψPG(ϕPG) = cPG(ϕPG) is given by
(14)with SP the average section crossed by the magnetic flux in the pole piece and SG the section of the flux in the air gap (see Fig. 10a). This corresponds to the serial connection of two magnetic capacitors: the first one is associated with the air gap G with linear constitutive law (as for the leakage flux ϕleak); the second one is associated with the pole piece P and cannot be described by a linear magnetic capacity due to the magnetic saturation that occurs in ferromagnetic material (see [32], Sect. 1). Those two serially-connected magnetic capacitors can merge into a single nonlinear capacitor that restores the total magnetomotive force ψPG(ϕPG). In this work, we consider the tangent-like constitutive relation detailed in Appendix C with flux saturation ϕsat = SP
bsat, where bsat depends on the specific magnetic material. From (C1) to (C3), the constitutive law ψPG(ϕPG) = cPG(ϕPG) is given by
 (15)where the coefficient
(15)where the coefficient  includes the contributions of both air and pole piece material, and
includes the contributions of both air and pole piece material, and  is a function shape parameter that depends on the specific material used for the pole piece. The associated (positive definite) storage function (C4) and (C5) is given by
is a function shape parameter that depends on the specific material used for the pole piece. The associated (positive definite) storage function (C4) and (C5) is given by
Again, any storage function suitable to a particular magnetic material could be used (such as those given in Appendix C), and the modular structure of the port-Hamiltonian formalism allows to change the storage function without modifying the interconnection matrix.
Steady state behavior
The permanent magnet is modeled as a constant source of magnetomotive force ψM (Ampere model [46]). This drives the magnetic flux in the path to an equilibrium (steady-state, ss) ϕPG = ϕss for which the magnetomotive force exactly compensates that of the magnet:
The associated steady-state magnetic capacity is the inverse of the linear approximation of ψPG(ϕPG) at ϕss:
 so that
so that  can be tuned according to
can be tuned according to
4.1.3 Eddy-currents losses
Besides the magnetic saturation, the pole piece is affected by the combination of capacitive and resistive effects due to eddy-currents, resulting in frequency-dependent losses. This phenomenon is well described by a linear fractional order magnetic capacity (see [3, 34, 47–50] and [48], part 5). This is out the scope of the present work and is postponed to a follow-up paper. Here, we consider a magnetic resistance Rec (Ω−1) with magnetic impedance
 (20)Since we consider a single magnetic flux in the pole piece ϕec = ϕPG, this impedance is serially connected to the magnetic capacity described in Section 4.1.2. The resulting structure is depicted in Figure 10b. Defining ωP = (Rec
Css)−1 (Hz) and
(20)Since we consider a single magnetic flux in the pole piece ϕec = ϕPG, this impedance is serially connected to the magnetic capacity described in Section 4.1.2. The resulting structure is depicted in Figure 10b. Defining ωP = (Rec
Css)−1 (Hz) and  (s), the resulting electrical impedance
(s), the resulting electrical impedance  is
is
4.1.4 Blocked electrical impedance
The current iC is common to (i) the resistor RC, (ii) the leakage inductance Lleak, and (iii) the impedance associated with the magnetic path in the coil core  . For a blocked coil
. For a blocked coil  , the total steady-state electrical impedance
, the total steady-state electrical impedance  measured at the coil terminals is given by
measured at the coil terminals is given by
The DC value (s = 0) is given by the resistance RC. In the high frequency range, the impedance is governed by the leakage inductance  . The inner bracket is the contribution of the proposed magnetic circuit.
. The inner bracket is the contribution of the proposed magnetic circuit.
4.1.5 Position-dependent force factor
The gyrator that restores the Lorentz force  with corresponding back electromotive force
with corresponding back electromotive force  is given by (see Eq. (B3) in Sect. B.2):
is given by (see Eq. (B3) in Sect. B.2):
 (23)with coil velocity
(23)with coil velocity  and
and  the length of coil wire effectively subjected to the magnetic field B. The apparent magnetic field B is modulated by the coil displacement (neglected in this work), and the length
the length of coil wire effectively subjected to the magnetic field B. The apparent magnetic field B is modulated by the coil displacement (neglected in this work), and the length  depends on the coil position (see Figs. 2.5–2.8 in [2] and Fig. 5 in [1]). We propose a parametric plateau function
depends on the coil position (see Figs. 2.5–2.8 in [2] and Fig. 5 in [1]). We propose a parametric plateau function  to model the latter phenomenon:
to model the latter phenomenon:
 (24)where
(24)where  is the total length of the coil,
is the total length of the coil,  describes the overhang of the coil with respect to the magnetic path (see Fig. 13a; and Sect. 3.1.2 from [1]), and
describes the overhang of the coil with respect to the magnetic path (see Fig. 13a; and Sect. 3.1.2 from [1]), and  is a shape parameter (see Fig. 13b).
is a shape parameter (see Fig. 13b).
 |
Figure 13 Effective length of coil wire |
4.2 Port-Hamiltonian formulation
The proposed loudspeaker modeling that includes electromagnetic phenomena (model 2) corresponds to the replacement of the inductance LC in model 0 by the electromagnetic circuit described in previous section (compare Figs. 2 and 12). It includes (i) the resistance-inductance circuit RC − Lleak serially connected to (ii) the magnetic circuit associated with the core of the coil and the magnet. This involves nx = 4 storage components (inductance Lleak, capacity cPG, mass MCDA, and stiffness KSA), nw = 3 dissipative components (resistances RC, RSA and Rec), and ny = 2 ports (voltage vI and magnetomotive force ψM). The state is  with the state associated with leakage flux
with the state associated with leakage flux  , and the Hamiltonian is
, and the Hamiltonian is  with
with  and
and  given in (16). The dissipation variable is
given in (16). The dissipation variable is  with linear dissipation law
with linear dissipation law  . According to (14), the magnetic induction in the air gap involved in the electromechanical coupling (B3) is
. According to (14), the magnetic induction in the air gap involved in the electromechanical coupling (B3) is  . The length of wire effectively subjected to the induction field is
. The length of wire effectively subjected to the induction field is  given in (24). The number of wire turns effectively surrounding the pole piece involved in the electromagnetic coupling is nP(x4) given in (13). With these definitions, the port-Hamiltonian formulation (3) of the loudspeaker model with the refined electromagnetic part (model 2 depicted in Fig. 10) is given in Table 4.
given in (24). The number of wire turns effectively surrounding the pole piece involved in the electromagnetic coupling is nP(x4) given in (13). With these definitions, the port-Hamiltonian formulation (3) of the loudspeaker model with the refined electromagnetic part (model 2 depicted in Fig. 10) is given in Table 4.
Blocks associated with the port-Hamiltonian formulation (3) for the loudspeaker model 2 depicted in Figure 10, where the Lorentz force factor is  with the magnetic induction in the air gap
with the magnetic induction in the air gap  and the position-dependent effective wire length
and the position-dependent effective wire length  defined in (24). See definitions and notations in Section 4.
defined in (24). See definitions and notations in Section 4.
4.3 Simulation results
The numerical method used to simulate model 2 is detailed in Appendix A. Physical parameters are given in Tables D1 and D3. In each case, the initial condition is the steady-state ϕPG(t = 0) = x2(t = 0) = ϕss.
Eddy-current losses
The effect of the characteristic time τec = 2πRec
Css due to eddy-currents in the pole piece is illustrated by imposing several DC input voltages vI, here −50 V, 0 V and +50 V (see evolution of flux ϕPG in Fig. 14), with the coil blocked at qD = 0 m and Css kept fixed, so that only Rec varies with τec. In each case, the magnetic flux in the path is driven to a new steady state  . The long-term effects and the influence of the characteristic time τPG are clearly visible.
. The long-term effects and the influence of the characteristic time τPG are clearly visible.
 |
Figure 14 Simulation of the loudspeaker model 2 in Table 4: Normalized flux |
Core saturation
The evolution of the small signal impedance with the steady-state is shown in Figure 15. First, the DC input voltages are imposed during 0.5 s. Second, a small signal noise is applied to evaluate the new steady-state blocked-impedance. We see an evolution in the high-frequency response according to the transfer function in (22). The associated value for is given in Css from (18) and the other parameters are given in Table D3.
 |
Figure 15 Simulation of the loudspeaker model 2 in Table 4: Evolution of the modulus of impedance |
Position-dependent electromagnetic coupling
To illustrate the effect of coil position on the electrical impedance, position qD in model 2 (Tab. 4) is fixed to −1 cm (inside), 0 cm (equilibrium) and +1 cm (outside). Due to the position-dependent effective number of coil wire (13), this changes the inductance according to (B6). Results are shown in Figure 16, in accordance with measurements in e.g. Fig. 6 from [1].
 |
Figure 16 Simulation of the loudspeaker model 2 in Table 4: Variation of impedance when the coil is blocked in different positions, hence changing the number of coil wire turns around the path nP(qD) and the inductance according to (B6). The flux is initially at ϕPG(t = 0) = ϕss. The sample-rate is 96 kHz. |
Flux-dependent force factor
The force factor in model 2  is modulated by the coil position (same as model 0) and the magnetic flux in the pole piece P and air gap G. This is clearly visible in the results of Figure 17: we observe that the force factor can be larger than predicted by the Thiele/Small modeling. Notice that the power balance is fulfilled.
is modulated by the coil position (same as model 0) and the magnetic flux in the pole piece P and air gap G. This is clearly visible in the results of Figure 17: we observe that the force factor can be larger than predicted by the Thiele/Small modeling. Notice that the power balance is fulfilled.
 |
Figure 17 Simulation of the model 2 in Table 4 depicted in Figure 12, for the parameters in Tables D1 and D3. The input voltage is a 100 Hz sine wave with increasing amplitude between 0 V and 50 V. The sampling rate is 96 kHz. The power balance is shown for the model 2 only. The force factor |
5 Conclusion
In this paper, a set of structures and components have been proposed to model well-known multiphysical phenomena occurring in loudspeakers, in view of system identification and correction. In particular, a finite-dimensional, power-balanced and passive-guaranteed time-domain formulation of viscoelastic and eddy-currents phenomena (linear) and material properties (stress–strain and b–h characteristics, nonlinear) have been derived. Those models are given in the framework of port-Hamiltonian systems, which decomposes the system into conservative, dissipative and source parts. The numerical method used for the simulations preserves this decomposition and thus is unconditionally stable. Numerical results that qualitatively comply with measured behaviors available in the literature have been presented.
The two loudspeaker models 1 and 2 have been developed independently of each other. This permits to illustrate the particular effect of each phenomenon on the loudspeaker dynamics. Now, their interconnection to form a global, multiphysical model that copes with all the phenomena covered in this work is straightforward, due to the modular nature of the port-Hamiltonian systems.
The first perspective of this work is to achieve DSP simulation-based real-time audio distortion compensation, based on the preliminary work in [7]. This requires the development of a parameter estimation method dedicated to the port-Hamiltonian structure. A second perspective is to include other phenomena that have not been considered here, such that the fractional dynamics associated with viscoelastic materials and eddy-currents, the acoustical load and the thermal evolution of the system. For all these issues, the modular structure of the proposed port-Hamiltonian models could be further exploited.
Conflict of interest
Author declared no conflict of interests.
Acknowledgments
This work is supported by the project ANR-16-CE92-0028, entitled Interconnected Infinite-Dimensional systems for Heterogeneous Media, INFIDHEM, financed by the French National Research Agency (ANR). Further information is available at https://websites.isae-supaero.fr/infidhem/the-project. The authors acknowledge Antonin Novak, Balbine Maillou (Laboratoire d’Acoustique de l’Université du Maine, UMR-CNRS 6613, Le Mans, France) for fruitful discussions on the loudspeaker mechanisms. The authors also acknowledge Robert Piéchaud for taking the time to complete the proofread of this paper.
Simulation code are available here: https://afalaize.github.io/posts/loudspeaker1/
References
- W. Klippel: Tutorial: Loudspeaker nonlinearities – causes, parameters, symptoms. Journal of the Audio Engineering Society 54 (2006) 907–939. [Google Scholar]
- B.R. Pedersen: Error correction of loudspeakers. PhD thesis, Aalborg University, Denmark, 2008. [Google Scholar]
- P. Brunet: Nonlinear system modeling and identification of loudspeakers. PhD thesis, Northeastern University Boston, 2014. [Google Scholar]
- J. Suykens, J. Vandewalle, J. Van Ginderdeuren: Feedback linearization of nonlinear distortion in electrodynamic loudspeakers. Journal of the Audio Engineering Society 43 (1995) 690–694. [Google Scholar]
- D. Jakobsson, M. Larsson: Modelling and compensation of nonlinear loudspeaker. Master’s Thesis, Department of Signals and Systems, Chalmers University of Technology, Sweden, 2010. [Google Scholar]
- M. Arvidsson, D. Karlsson: Attenuation of Harmonic Distortion in Loudspeakers Using Non-Linear Control. Institutionen för systemteknik, Linköping, 2012. [Google Scholar]
- A. Falaize, N. Papazoglou, T. Hélie, N. Lopes: Compensation of loudspeaker’s nonlinearities based on flatness and port-Hamiltonian approach, in 22ème Congrès Français de Mécanique, Lyon, France, August 2015. Association Française de Mécanique, 2015. [Google Scholar]
- S. Tassart, S. Valcin, M. Menu: Active loudspeaker heat protection. Journal of the Audio Engineering Society 62 (2014) 767–775. [CrossRef] [Google Scholar]
- N. Thiele: Loudspeakers in vented boxes: Part 1. Journal of the Audio Engineering Society 19 (1971) 382–392. [Google Scholar]
- N. Thiele: Loudspeakers in vented boxes: Part 2. Journal of the Audio Engineering Society 19 (1971) 471–483. [Google Scholar]
- R.H. Small: Closed-box loudspeaker systems-part 1: analysis. Journal of the Audio Engineering Society 20 (1972) 798–808. [Google Scholar]
- R.H. Small: Closed-box loudspeaker systems-part 2: Synthesis. Journal of the Audio Engineering Society 21 (1973) 11–18. [Google Scholar]
- P.J. Chapman: Thermal simulation of loudspeakers, in Audio Engineering Society Convention 104. Audio Engineering Society, 1998. [Google Scholar]
- W. Marshall Leach Jr.: Loudspeaker voice-coil inductance losses: circuit models, parameter estimation, and effect on frequency response. Journal of the Audio Engineering Society 50 (2002) 442–450. [Google Scholar]
- W. Klippel: Nonlinear modeling of the heat transfer in loudspeakers. Journal of the Audio Engineering Society 52 (2004) 3–25. [Google Scholar]
- K. Thorborg, A.D. Unruh, C.J. Struck: An improved electrical equivalent circuit model for dynamic moving coil transducers. Audio Engineering Society Convention 122 (2007). [Google Scholar]
- K. Thorborg, C. Tinggaard, F. Agerkvist, C. Futtrup: Frequency dependence of damping and compliance in loudspeaker suspensions. Journal of the Audio Engineering Society 58 (2010) 472–486. [Google Scholar]
- F.T. Agerkvist: Non-linear viscoelastic models, in Audio Engineering Society Convention 131, New York, NY, Audio Engineering Society. 2011. [Google Scholar]
- W. Klippel: Dynamic measurement and interpretation of the nonlinear parameters of electrodynamic loudspeakers. Journal of the Audio Engineering Society 38 (1990) 944–955. [Google Scholar]
- M.R. Bai, C.M. Huang: Expert diagnostic system for moving-coil loudspeakers using nonlinear modeling. The Journal of the Acoustical Society of America 125 (2009) 819–830. [CrossRef] [PubMed] [Google Scholar]
- A.J.M. Kaizer: Modeling of the nonlinear response of an electrodynamic loudspeaker by a volterra series expansion. Journal of the Audio Engineering Society 35 (1987) 421–433. [Google Scholar]
- S. Brown: Linear and nonlinear loudspeaker characterization. PhD thesis, Citeseer, 2006. [Google Scholar]
- K. Lashkari: A novel volterra-wiener model for equalization of loudspeaker distortions, in Acoustics, Speech and Signal Processing, 2006. ICASSP 2006 Proceedings. 2006 IEEE International Conference on, Vol. 5, IEEE, 2006, pp. V–V. [Google Scholar]
- P. Brunet, B. Shafai: State-space modeling and identification of loudspeaker with nonlinear distortion, in Modelling, Identification, and Simulation, IASTED International Conference on, Vol. 755. 2011. [Google Scholar]
- M. Soria-Rodríguez, M. Gabbouj, N. Zacharov, M.S. Hämäläinen, K. Koivuniemi: Modeling and real-time auralization of electrodynamic loudspeaker non-linearities, in Acoustics, Speech, and Signal Processing, 2004. Proceedings (ICASSP’04). IEEE International Conference on, Vol. 4, IEEE, 2004, pp. iv–81. [Google Scholar]
- B.M. Maschke, A.J. Van Der Schaft, P.C. Breedveld: An intrinsic hamiltonian formulation of network dynamics: Non-standard poisson structures and gyrators. Journal of the Franklin Institute 329 (1992) 923–966. [Google Scholar]
- A. van der Schaft: Port-Hamiltonian systems: an introductory survey. Proceedings oh the International Congress of Mathematicians 3 (2006) 1339–1366. [Google Scholar]
- V. Duindam, A. Macchelli, S. Stramigioli, H. Bruyninckx: Modeling and control of complex physical systems: The Port-Hamiltonian approach. Springer Science & Business Media, 2009. [CrossRef] [Google Scholar]
- A. Falaize, T. Hélie: Passive guaranteed simulation of analog audio circuits: A port-Hamiltonian approach. Applied Sciences 6 (2016) 273. [CrossRef] [Google Scholar]
- M.H. Knudsen, J.G. Jensen: Low-frequency loudspeaker models that include suspension creep. Journal of the Audio Engineering Society 41 (1993) 3–18. [Google Scholar]
- B.R. Pedersen, F.T. Agerkvist: Time varying behavior of the loudspeaker suspension, in Audio Engineering Society Convention 123. Audio Engineering Society, 2007. [Google Scholar]
- M. Getzlaff: Fundamentals of magnetism. Springer Science & Business Media, 2007. [Google Scholar]
- V. François-Lavet, F. Henrotte, L. Stainer, L. Noels, C. Geuzaine: Vectorial incremental nonconservative consistent hysteresis model, in Proceedings of the 5th International Conference on Advanded COmputational Methods in Engineering (ACOMEN2011), 2011. [Google Scholar]
- A. Rumeau: Modélisation comportementale en génie électrique sous représentation diffusive: méthodes et applications. PhD thesis, Université de Toulouse, Université Toulouse III-Paul Sabatier, 2009. [Google Scholar]
- A. Falaize: Pyphs: A Python software (Py) dedicated to the simulation of multi-physical Port-Hamiltonian Systems (PHS) described by graph structures. https://github.com/pyphs/pyphs, accessed 21st of Decemeber, 2016. [Google Scholar]
- J.-J.E. Slotine, W. Li, et al.: Applied Nonlinear Control, Vol. 199. Prentice-Hall, Englewood Cliffs, NJ, 1991. [Google Scholar]
- F.T. Agerkvist, T. Ritter: Modeling viscoelasticity of loudspeaker suspensions using retardation spectra, in Audio Engineering Society Convention 129, New York, NY, Audio Engineering Society. 2010. [Google Scholar]
- R.C. Koeller: Applications of fractional calculus to the theory of viscoelasticity. Journal of Applied Mechanics 51 (1984) 299–307. [Google Scholar]
- R. Lewandowski, B. Chorażyczewski: Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Computers & Structures 88 (2010) 1–17. [Google Scholar]
- W.N. Findley, F.A. Davis: Creep and relaxation of nonlinear viscoelastic materials. Courier Corporation, 2013. [Google Scholar]
- J. Vanderkooy: A model of loudspeaker driver impedance incorporating eddy currents in the pole structure, in Audio Engineering Society Convention 84. Audio Engineering Society, 1988. [Google Scholar]
- J.R. Wright: An empirical model for loudspeaker motor impedance. Journal of the Audio Engineering Society 38 (1990) 749–754. [Google Scholar]
- M. Dodd, W. Klippel, J. Oclee-Brown: Voice coil impedance as a function of frequency and displacement, in Audio Engineering Society Convention 117. Audio Engineering Society, 2004. [Google Scholar]
- X.-P. Kong, F. Agerkvist, X.-W. Zeng: Modeling of lossy inductance in moving-coil loudspeakers. Acta Acustica United With Acustica 101 (2015). [Google Scholar]
- R. Buntenbach: A generalized circuit model for multiwinding inductive devices. Magnetics, IEEE Transactions on 6 (1970) 65–65. [CrossRef] [Google Scholar]
- D.C. Hamill: Lumped equivalent circuits of magnetic components: the gyrator-capacitor approach. Power Electronics, IEEE Transactions on 8 (1993) 97–103. [CrossRef] [Google Scholar]
- L. Laudebat: Modélisation et identification sous représentation diffusive de comportements dynamiques non rationnels en génie électrique. Thèse de l’Université Paul Sabatier, Toulouse, 2003. [Google Scholar]
- J. Sabatier, O.P. Agrawal, J.A. Tenreiro Machado: Advances in Fractional Calculus, Vol. 4. Springer, 2007. [CrossRef] [Google Scholar]
- I. Schäfer, K. Krüger: Modelling of lossy coils using fractional derivatives. Journal of Physics D: Applied Physics 41 (2008) 045001. [Google Scholar]
- P. Brunet, B. Shafai: Identification of loudspeakers using fractional derivatives. Journal of the Audio Engineering Society 62 (2014) 505–515. [CrossRef] [Google Scholar]
- T. Itoh, K. Abe: Hamiltonian-conserving discrete canonical equations based on variational difference quotients, Journal of Computational Physics 76 (1988) 85–102. [Google Scholar]
- N. Lopes, T. Hélie, A. Falaize: Explicit second-order accurate method for the passive guaranteed simulation of port-Hamiltonian systems. IFAC-PapersOnLine 48 (2015) 223–228. [CrossRef] [Google Scholar]
Appendix A: Numerical method
In this section, we present the numerical method used in this paper for the simulation of models 0, 1 and 2. It is based on the appropriate definition of a discrete gradient [51] which restores the passive-guaranteed port-Hamiltonian structure (3) in discrete time so that numerical stability is guaranteed (see [29, 52] for details, in particular for an analysis of consistency of the method which respect to the time step, which we do not recall here).
To ensure stable simulation of stable dynamical system  , many numerical schemes focus on the approximation quality of the time derivative, combined with operation of the vector field f. Here, we adopt an alternative point of view, by transposing the power balance (4) in the discrete time-domain to preserve passivity. This is achieved by numerical schemes that provide a discrete version of the chain rule for computing the derivative of
, many numerical schemes focus on the approximation quality of the time derivative, combined with operation of the vector field f. Here, we adopt an alternative point of view, by transposing the power balance (4) in the discrete time-domain to preserve passivity. This is achieved by numerical schemes that provide a discrete version of the chain rule for computing the derivative of  . This is the case of Euler scheme, for which first order approximation of the differential applications
. This is the case of Euler scheme, for which first order approximation of the differential applications  and dH(x, dx) = ∇H(x)Tdx on the sample grid
and dH(x, dx) = ∇H(x)Tdx on the sample grid  are given by
are given by
For mono-variate storage components ( ), the solution can be built element-wise with the n-th coordinate given by
), the solution can be built element-wise with the n-th coordinate given by
A discrete chain rule is indeed recovered
 (A4)so that the following substitution in (3)
(A4)so that the following substitution in (3)
For pH systems composed of a collection of linear energy storing components with quadratic Hamiltonian  , we define
, we define  so that the discrete gradient (A3) reads
so that the discrete gradient (A3) reads
 (A7)which restores the midpoint rule. For nonlinear case, (A3) does not coincide with the mid-point rule anymore, still preserving passivity due to equation (A6) which does not assume the system linearity.
(A7)which restores the midpoint rule. For nonlinear case, (A3) does not coincide with the mid-point rule anymore, still preserving passivity due to equation (A6) which does not assume the system linearity.
Remark A.1 (Nonlinear solver). The proposed method guarantees the passivity of the discrete time model provided the resulting nonlinear implicit equations are solved exactly. This depends on the nonlinear solver at hand but not on the proposed method.
Appendix B: Recalls on magnetism
In this section, we give the elements for the modeling of lumped electromagnetic systems in the pH formalism. First, the closed-form expression for energy storage is recalled. Second and third, we give the port-Hamiltonian formulation of electromechanical and electromagnetic coupling, respectively.
B.1 Magnetic energy storage
Definitions
The magnetic phenomena are described by two complementary fields, namely, the applied magnetic excitation h and the induced magnetic flux density b(h), which is somewhat the response of a given material to a given excitation. The induction b is defined as the superposition of the magnetization of vacuum j0(h) and the magnetization of matter j(h) due to microscopic magnetic moments attached to the atoms of the body (see Eq. (1.6) from [32] and Eq. (6) from [33]):
 where we neglect the magnetization of vacuum so that h(b) = j−1(b). The magnetic induction flux ϕ is defined as the flux of the magnetic induction field through a given surface
where we neglect the magnetization of vacuum so that h(b) = j−1(b). The magnetic induction flux ϕ is defined as the flux of the magnetic induction field through a given surface  , where b(t) is the magnitude of the field b(t) that we assume constant over
, where b(t) is the magnitude of the field b(t) that we assume constant over  and normal to the cross section. The magnetomotive force ψ is defined as the circulation of h along a closed b-field line
and normal to the cross section. The magnetomotive force ψ is defined as the circulation of h along a closed b-field line  with length
with length  , where we assume h(b(t)) constant along
, where we assume h(b(t)) constant along  .
.
Energy storage
The variation of magnetic energy density (locally) stored in a sample of magnetic material is  (see e.g. [33] for details). Again assuming that h is constant over the b-field line and b constant over a cross section of the material, the variation of the total energy for a sample with length
(see e.g. [33] for details). Again assuming that h is constant over the b-field line and b constant over a cross section of the material, the variation of the total energy for a sample with length  and cross section S is
and cross section S is  . Rewriting the preceding relation for the magnetic flux ϕ = Sb and the magnetomotive force
. Rewriting the preceding relation for the magnetic flux ϕ = Sb and the magnetomotive force  yields
yields  . Thus, we can select ϕ as the state associated with the storage of magnetic energy with E(t) = Hmag(ϕ(t)) and we identify
. Thus, we can select ϕ as the state associated with the storage of magnetic energy with E(t) = Hmag(ϕ(t)) and we identify  :
:
 (B1)with the total energy variation
(B1)with the total energy variation  .
.
B.2 Electromechanical coupling
Consider several windings of a conductive wire with section SW, total length  , position qW and velocity vector v
W = vW
e
W with constant direction e
W and magnitude
, position qW and velocity vector v
W = vW
e
W with constant direction e
W and magnitude  . This conductor is immersed in a magnetic induction field b with constant direction orthogonal to e
W and constant magnitude B. The current is
. This conductor is immersed in a magnetic induction field b with constant direction orthogonal to e
W and constant magnitude B. The current is  for the electric charge density ρq
moving inside the wire at velocity v
q
= vq
e
q
with unitary vector e
q
normal to a cross section of the wire. A wire element with length
for the electric charge density ρq
moving inside the wire at velocity v
q
= vq
e
q
with unitary vector e
q
normal to a cross section of the wire. A wire element with length  is subjected to the Lorentz force
is subjected to the Lorentz force  . This force is orthogonal to the velocity v
q + v
W so that the associated mechanical power is
. This force is orthogonal to the velocity v
q + v
W so that the associated mechanical power is  . Integrating along the wire, one gets
. Integrating along the wire, one gets
 (B2)defining the Lorentz force
(B2)defining the Lorentz force  and the back electromotive force (voltage)
and the back electromotive force (voltage)  . Notice the transfer is reversible and conservative in the sense that the outflow of energy from the electrical domain
. Notice the transfer is reversible and conservative in the sense that the outflow of energy from the electrical domain  equals the inflow of the mechanical domain
equals the inflow of the mechanical domain  . This corresponds to a gyrator with ratio
. This corresponds to a gyrator with ratio  :
:
 (B4)since the interconnection matrix is skew-symmetric.
(B4)since the interconnection matrix is skew-symmetric.
B.3 Electromagnetic coupling: the gyrator-capacitor approach
The gyrator-capacitor approach introduced in the late sixties [45, 46] is an easy way to develop electronic analog of magnetic circuits. It has been considered in [14] for the modeling of the loudspeaker. In this approach, a coil is divided in a gyrator (wire turns) and a magnetic energy storage (coil core).
The dynamics of a magnetic field can be described by two complementary macroscopic quantities: the magnetic induction flux ϕ and the magnetomotive force (mmf) ψ (see Sect. B.1). The electromagnetic transfer for a single wire turn stands from (i) Faraday’s law of electromagnetic induction that relates the electromotive force (voltage υ) to the variation of the magnetic flux in the wire turn  ; and (ii) Ampere’s theorem that relates the mmf to the current in the wire ψ = i (see [45, 46]). Considering a coil (C) with NC wire turns around the path (P), these relations restore a gyrator with ratio NC:
; and (ii) Ampere’s theorem that relates the mmf to the current in the wire ψ = i (see [45, 46]). Considering a coil (C) with NC wire turns around the path (P), these relations restore a gyrator with ratio NC:
Denoting by  the Laplace variable, the correspondence between an impedance seen in the electrical domain
the Laplace variable, the correspondence between an impedance seen in the electrical domain  and its counterpart in the magnetic domain
and its counterpart in the magnetic domain  is given by
is given by
As a result, if the path (P) is modeled by a magnetic capacity CP, e.g. from the linearization of  in (B1), the equivalent electrical inductance is
in (B1), the equivalent electrical inductance is  . Notice the interconnection (B5) is conservative: Pelec = Pmag with Pelec = vC
iC the power outgoing the electrical domain and
. Notice the interconnection (B5) is conservative: Pelec = Pmag with Pelec = vC
iC the power outgoing the electrical domain and  the power incoming the magnetic domain.
the power incoming the magnetic domain.
Appendix C: Storage functions
In this section, we precise the requirements on storage functions and detail the saturating storage functions we use in the loudspeakers models.
Requirements for storage functions
As stated in Section 2.2, the requirement for elementary storage function (Hamiltonian)  are as follows:
are as follows:
It is positive semidefinite: H(x) ≥ 0,
 ;
;It is zero at origin: H(0) = 0;
It is radially unbounded:
 with
with  the boundary of domain
the boundary of domain  (could be {±∞};
(could be {±∞};Its second derivative is positive:
 ,
,  .
.
Requirements (1) and (2) ensure the associated energy  is always positive or null; requirement (3) ensures the origin x = 0 is an attractor for the associated dynamical system from LaSalle invariance theroem; finally, requirement (4) ensures the derivative is monotonically increasing so that it invertible on its domain
is always positive or null; requirement (3) ensures the origin x = 0 is an attractor for the associated dynamical system from LaSalle invariance theroem; finally, requirement (4) ensures the derivative is monotonically increasing so that it invertible on its domain  . A simple procedure to build such storage function is to integrate twice a non-vanishing, positive definite function
. A simple procedure to build such storage function is to integrate twice a non-vanishing, positive definite function  ,
,  , choosing the two integration constants
, choosing the two integration constants  so that
so that  and
and  are both null at x = 0. Note that it is not required the storage function to be symmetric with possibly
are both null at x = 0. Note that it is not required the storage function to be symmetric with possibly  . Some examples are given below (see also Fig. C1).
. Some examples are given below (see also Fig. C1).
 |
Figure C1 Examples of storage functions detailed in Section C with their respective derivative. quad: quadratic storage function; poly: polynomial storage function; exp: Non-symmetric exponential-based storage function; sat: saturating storage function. The parameters are chosen arbitrarily. |
Examples of storage functions
Quadratic: The simplest storage functions are the quadratic functions
 , with (linear) derivative H′(x) = px.
, with (linear) derivative H′(x) = px.Polynomial: It is possible to construct polynomial storage function with only even order to ensure the requirements are satisfied, e.g.
 , with derivative
, with derivative  .
.
Non-symmetric
A non symmetric storage functions can be constructed from two exponential functions as follows:  with derivative
with derivative  , where possibly
, where possibly  .
.
State saturating storage functions
In this work, the saturation effect of the suspension and the ferromagnetic path are described by the same idealized (symmetric) saturation curve c(x). It is built as the linear combination of basis functions clin(x) (linear behavior around the origin) and csat(x) (saturation effect):
 (C3)with
(C3)with  ,
,  so that csat(x) does not contribute around origin, and
so that csat(x) does not contribute around origin, and  .
.
The corresponding Hamiltonian is obtained from
This nonlinear saturating storage function proves positive definite providing the parameters (Plin, Psat) are positive, so that it can be used in structure (3), still preserving passivity.
Appendix D: Physical and technological parameters
Acronym d.u. stands for dimensionless unit
Cite this article as: A. Falaize & T. Hélie. 2020. Passive modelling of the electrodynamic loudspeaker: from the Thiele–Small model to nonlinear port-Hamiltonian systems. Acta Acustica, 4, 1.
All Tables
Port-Hamiltonian formulation (3) for the model 1 depicted in Figure 6. The linear stiffness  is replaced by the Kelvin–Voigt modeling of the creep effect from Section 3.1 in serial connection with the nonlinear spring described in Section 3.2, with diaphragm position
is replaced by the Kelvin–Voigt modeling of the creep effect from Section 3.1 in serial connection with the nonlinear spring described in Section 3.2, with diaphragm position  , momentum
, momentum  , primary elongation
, primary elongation  , and creep elongation
, and creep elongation  . The nonlinear potential energy
. The nonlinear potential energy  is given in (11). Parameters are given in Tables 4 and D1, with
is given in (11). Parameters are given in Tables 4 and D1, with  and
and  .
.
Blocks associated with the port-Hamiltonian formulation (3) for the loudspeaker model 2 depicted in Figure 10, where the Lorentz force factor is  with the magnetic induction in the air gap
with the magnetic induction in the air gap  and the position-dependent effective wire length
and the position-dependent effective wire length  defined in (24). See definitions and notations in Section 4.
defined in (24). See definitions and notations in Section 4.
All Figures
 |
Figure 1 Schematic of the electrodynamic loudspeaker and components labels. |
| In the text | |
 |
Figure 2 Equivalent circuit with direct electromechanical analogy (force ↔ voltage, velocity ↔ current) that corresponds to the Thiele–Small model (1) and (2) with electromechanical coupling |
| In the text | |
 |
Figure 3 Simulation results for the model 0 in Table 1. Physical parameters are given in Table D1. The input voltage vI is a 100 Hz sine wave with increasing amplitude between 0 and 50 V. The sampling rate is Fs = 96 kHz. |
| In the text | |
 |
Figure 4 Transfer functions from the simulation of the model 0 in Table 1 (phs) and computed from filter theory (target). Physical parameters are given in Table D1. The input voltage vI is a 1 V white noise and the sampling rate is Fs = 96 kHz. |
| In the text | |
 |
Figure 5 Small-signal modeling of the mechanical part which includes: the total mass MCDA (diaphragm, coil and additional mass due to acoustic radiation), the fluid-like damper RSA (mechanical friction and small signal approximation for the acoustic power radiation), primary stiffness K0 and Kelvin–Voigt modeling of the creep effect (K1, R1), with diaphragm position qD, primary elongation q0 and creep elongation q1. Parameters are given in Tables D1 and D2. |
| In the text | |
 |
Figure 6 Equivalent circuit for model 1 with diaphragm position qD, primary elongation q0 and creep elongation q1. Elements common to model 0 in Figure 2 are shaded. |
| In the text | |
 |
Figure 7 Simulation of the small-signal modeling of the mechanical subsystem in Table 2: Compliance in the frequency domain (diaphragm displacement in response to the Lorentz force |
| In the text | |
 |
Figure 8 Simulation of the small-signal modeling of the mechanical subsystem in Table 2: diaphragm displacement in response to a 10N Lorentz force step between 0s and 2s (time domain). Note that τve = 0 corresponds to the mechanical subsystem as described by the Thiele–Small model (no creep). |
| In the text | |
 |
Figure 9 Simulation of the model 1 in Table 3 depicted in Figure 6, for the parameters in Tables D1 and D2 (except |
| In the text | |
 |
Figure 10 Proposed modeling of the electromagnetic circuit, which includes: the coil wire resistance RC, the linear inductance associated with the leakage flux ϕleak, the electromagnetic transduction with nP the number of wire turns around the magnetic path, the magnetic energy storage in the ferromagnetic path described by the nonlinear induction–excitation curve ψPG(ϕPG) from (15), the linear dissipation associated with eddy-currents in the pole piece, and the constant source of magnetomotive force ψM due to the magnet from (17). |
| In the text | |
 |
Figure 11 Plot of the position-dependent effective number of wire turns nP(qD) involved in the electromagnetic coupling from (13) with q+ = 5 mm and q− in the legend. |
| In the text | |
 |
Figure 12 Equivalent circuit of the model 2 described in Table 4. Elements common to model 0 in Figure 2 are shaded. The coil inductance LC is replaced by the electromagnetic circuit from Figure 10b which includes the leakage inductance Lleak and the magnetic path (pole piece P and air gap G). |
| In the text | |
 |
Figure 13 Effective length of coil wire |
| In the text | |
 |
Figure 14 Simulation of the loudspeaker model 2 in Table 4: Normalized flux |
| In the text | |
 |
Figure 15 Simulation of the loudspeaker model 2 in Table 4: Evolution of the modulus of impedance |
| In the text | |
 |
Figure 16 Simulation of the loudspeaker model 2 in Table 4: Variation of impedance when the coil is blocked in different positions, hence changing the number of coil wire turns around the path nP(qD) and the inductance according to (B6). The flux is initially at ϕPG(t = 0) = ϕss. The sample-rate is 96 kHz. |
| In the text | |
 |
Figure 17 Simulation of the model 2 in Table 4 depicted in Figure 12, for the parameters in Tables D1 and D3. The input voltage is a 100 Hz sine wave with increasing amplitude between 0 V and 50 V. The sampling rate is 96 kHz. The power balance is shown for the model 2 only. The force factor |
| In the text | |
 |
Figure C1 Examples of storage functions detailed in Section C with their respective derivative. quad: quadratic storage function; poly: polynomial storage function; exp: Non-symmetric exponential-based storage function; sat: saturating storage function. The parameters are chosen arbitrarily. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.
















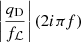

























![$$ [{\nabla }_dH(\mathbf{x},\mathbf{x}+\delta \mathbf{x}){]}_n=\left\{\begin{array}{ll}\frac{{h}_n({x}_n+\delta {x}_n)-{h}_n({x}_n)}{\delta {x}_n}& \mathrm{if}\enspace \delta {x}_n\ne 0,\\ {h}_n^\mathrm{\prime}({x}_n)& \enspace \mathrm{otherwise}\enspace.\end{array}\right. $$](/articles/aacus/full_html/2020/01/aacus190001s/aacus190001s-eq129.gif)

}}+\underset{{\mathrm{P}}_{\mathrm{D}}(k)}{\underbrace{\mathbf{z}(\mathbf{w}(k){)}^{\mathrm{T}}\enspace \mathbf{w}(k)}}-\underset{{\mathrm{P}}_{\mathrm{S}}(k)}{\underbrace{\mathbf{u}(k{)}^{\mathrm{T}}\enspace \mathbf{y}(k)}}.\end{array} $$](/articles/aacus/full_html/2020/01/aacus190001s/aacus190001s-eq132.gif)






